
科目: 来源: 题型:
【题目】过![]() 轴正半轴上一点
轴正半轴上一点![]() 做直线与抛物线
做直线与抛物线![]() 交于
交于![]() ,
,![]() ,
,![]() 两点,且满足
两点,且满足![]() ,过定点
,过定点![]() 与点
与点![]() 做直线
做直线![]() 与抛物线交于另一点
与抛物线交于另一点![]() ,过点
,过点![]() 与点
与点![]() 做直线
做直线![]() 与抛物线交于另一点
与抛物线交于另一点![]() .设三角形
.设三角形![]() 的面积为
的面积为![]() ,三角形
,三角形![]() 的面积为
的面积为![]() .
.
(1)求正实数![]() 的取值范围;
的取值范围;
(2)连接![]() ,
,![]() 两点,设直线
两点,设直线![]() 的斜率为
的斜率为![]() ;
;
(ⅰ)当![]() 时,直线
时,直线![]() 在
在![]() 轴的纵截距范围为
轴的纵截距范围为![]() ,则求
,则求![]() 的取值范围;
的取值范围;
(ⅱ)当实数![]() 在(1)取到的范围内取值时,求
在(1)取到的范围内取值时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】哈三中总务处的老师要购买学校教学用的粉笔,并且有非常明确的判断一盒粉笔是“优质产品”和“非优质产品”的方法.某品牌的粉笔整箱出售,每箱共有20盒,根据以往的经验,其中会有某些盒的粉笔为非优质产品,其余的都为优质产品.并且每箱含有0,1,2盒非优质产品粉笔的概率为0.7,0.2和0.1.为了购买该品牌的粉笔,校总务主任设计了一种购买的方案:欲买一箱粉笔,随机查看该箱的4盒粉笔,如果没有非优质产品,则购买,否则不购买.设“买下所查看的一箱粉笔”为事件![]() ,“箱中有
,“箱中有![]() 件非优质产品”为事件
件非优质产品”为事件![]() .
.
(1)求![]() ,
,![]() ,
,![]() ;
;
(2)随机查看该品牌粉笔某一箱中的四盒,设![]() 为非优质产品的盒数,求
为非优质产品的盒数,求![]() 的分布列及期望;
的分布列及期望;
(3)若购买100箱该品牌粉笔,如果按照主任所设计方案购买的粉笔中,箱中每盒粉笔都是优质产品的箱数的期望比随机购买的箱中每盒粉笔都是优质产品的箱数的期望大10,则所设计的方案有效.讨论该方案是否有效.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() ,曲线
,曲线![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求![]() 的极坐标方程;
的极坐标方程;
(2)射线![]() 的极坐标方程为
的极坐标方程为![]() ,若
,若![]() 分别与
分别与![]() 交于异于极点的
交于异于极点的![]() 两点,求
两点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某科研团队对![]() 例新冠肺炎确诊患者的临床特征进行了回顾性分析.其中
例新冠肺炎确诊患者的临床特征进行了回顾性分析.其中![]() 名吸烟患者中,重症人数为
名吸烟患者中,重症人数为![]() 人,重症比例约为
人,重症比例约为![]() ;
;![]() 名非吸烟患者中,重症人数为
名非吸烟患者中,重症人数为![]() 人,重症比例为
人,重症比例为![]() .
.
(1)根据以上数据完成![]() 列联表;
列联表;
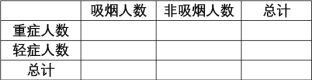
(2)根据(1)中列联表数据,能否在犯错误的概率不超过![]() 的前提下认为新冠肺炎重症与吸烟有关?
的前提下认为新冠肺炎重症与吸烟有关?
(3)已知每例重症患者平均治疗费用约为![]() 万元,每例轻症患者平均治疗费用约为
万元,每例轻症患者平均治疗费用约为![]() 万元.根据(1)中列联表数据,分别求吸烟患者和非吸烟患者的平均治疗费用.(结果保留两位小数)
万元.根据(1)中列联表数据,分别求吸烟患者和非吸烟患者的平均治疗费用.(结果保留两位小数)
附:
|
|
|
|
|
|
|
|
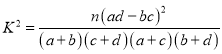
查看答案和解析>>
科目: 来源: 题型:
【题目】某商场推出消费抽现金活动,顾客消费满1000元可以参与一次抽奖,该活动设置了一等奖、二等奖、三等奖以及参与奖,奖金分别为:一等奖200元、二等奖100元、三等奖50元、参与奖20元,具体获奖人数比例分配如图,则下列说法中错误的是( )

A.获得参与奖的人数最多
B.各个奖项中一等奖的总金额最高
C.二等奖获奖人数是一等奖获奖人数的两倍
D.奖金平均数为![]() 元
元
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() ,曲线
,曲线![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求![]() 的极坐标方程;
的极坐标方程;
(2)射线![]() 的极坐标方程为
的极坐标方程为![]() ,若
,若![]() 分别与
分别与![]() 交于异于极点的
交于异于极点的![]() 两点,求
两点,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com