
科目: 来源: 题型:
【题目】已知椭圆![]() 的右焦点为F,直线l与C交于M,N两点.
的右焦点为F,直线l与C交于M,N两点.
(1)若l过点F,点M,N到直线y=2的距离分别为d1,d2,且![]() ,求l的方程;
,求l的方程;
(2)若点M的坐标为(0,1),直线m过点M交C于另一点N′,当直线l与m的斜率之和为2时,证明:直线NN′过定点.
查看答案和解析>>
科目: 来源: 题型:
【题目】某总公司在A,B两地分别有甲、乙两个下属公司同时生产某种新能源产品(这两个公司每天都固定生产50件产品),所生产的产品均在本地销售.产品进入市场之前需要对产品进行性能检测,得分低于80分的定为次品,需要返厂再加工;得分不低于80分的定为正品,可以进入市场.检测员统计了甲、乙两个下属公司100天的生产情况及每件产品盈利亏损情况,数据如下表所示:
表1:
甲公司 | 得分 |
|
|
|
|
|
件数 | 10 | 10 | 40 | 40 | 50 | |
天数 | 10 | 10 | 10 | 10 | 80 |
表2:
乙公司 | 得分 |
|
|
|
| |
件数 | 10 | 5 | 40 | 45 | 50 | |
天数 | 20 | 10 | 20 | 10 | 70 |
表3:
每件正品 | 每件次品 | |
甲公司 | 盈2万元 | 亏3万元 |
乙公司 | 盈3万元 | 亏3.5万元 |
(1)分别求甲、乙两个公司这100天生产的产品的正品率(用百分数表示);
(2)试问甲乙两个公司这100天生产的产品的总利润哪个更大?说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校拟从甲、乙两名同学中选一人参加疫情知识问答竞赛,于是抽取了甲、乙两人最近同时参加校内竞赛的十次成绩,将统计情况绘制成如图所示的折线图.根据该折线图,下面结论正确的是( )
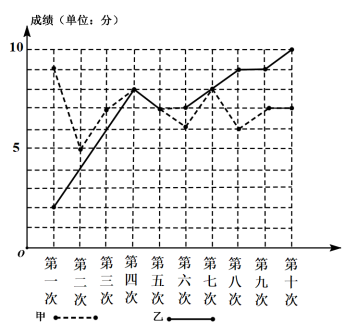
A.甲、乙成绩的中位数均为7
B.乙的成绩的平均分为6.8
C.甲从第四次到第六次成绩的下降速率要大于乙从第四次到第五次的下降速率
D.甲的成绩的方差小于乙的成绩的方差
查看答案和解析>>
科目: 来源: 题型:
【题目】若无穷数列![]() 满足:存在
满足:存在![]() ,对任意的
,对任意的![]() ,都有
,都有![]() (
(![]() 为常数),则称
为常数),则称![]() 具有性质
具有性质![]()
(1)若无穷数列![]() 具有性质
具有性质![]() ,且
,且![]() ,求
,求![]() 的值
的值
(2)若无穷数列![]() 是等差数列,无穷数列
是等差数列,无穷数列![]() 是公比为正数的等比数列,
是公比为正数的等比数列,![]() ,
,![]() ,
,![]() ,判断
,判断![]() 是否具有性质
是否具有性质![]() ,并说明理由.
,并说明理由.
(3)设无穷数列![]() 既具有性质
既具有性质![]() ,又具有性质
,又具有性质![]() ,其中
,其中![]() 互质,求证:数列
互质,求证:数列![]() 具有性质
具有性质![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知动直线与![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两不同点,且
两不同点,且![]() 的面积
的面积![]() ,其中
,其中![]() 为坐标原点
为坐标原点
(1)若动直线![]() 垂直于
垂直于![]() 轴.求直线
轴.求直线![]() 的方程;
的方程;
(2)证明:![]() 和
和![]() 均为定值;
均为定值;
(3)椭圆![]() 上是否存在点
上是否存在点![]() ,
,![]() ,
,![]() ,使得三角形面积
,使得三角形面积![]() 若存在,判断
若存在,判断![]() 的形状;若不存在,请说明理由
的形状;若不存在,请说明理由
查看答案和解析>>
科目: 来源: 题型:
【题目】随着疫情的有效控制,人们的生产生活逐渐向正常秩序恢复,位于我区的某著名赏花园区重新开放.据统计硏究,近期每天赏花的人数大致符合以下数学模型![]() .以
.以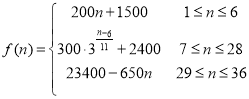 表示第
表示第![]() 个时刻进入园区的人数,以
个时刻进入园区的人数,以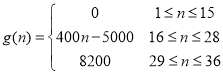 表示第
表示第![]() 个时刻离开园区的人数,设定每15分钟为一个计算单位,上午8点15分作为第1个计算人数单位,即
个时刻离开园区的人数,设定每15分钟为一个计算单位,上午8点15分作为第1个计算人数单位,即![]() 点30分作为第2个计算单位,即
点30分作为第2个计算单位,即![]() :依次类推,把一天内从上午8点到下午5点分成36个计算单位(最后结果四舍五入,精确到整数)
:依次类推,把一天内从上午8点到下午5点分成36个计算单位(最后结果四舍五入,精确到整数)
(1)试分别计算当天12:30至13:30这一小时内,进入园区的人数![]() 和离开园区的游客人数
和离开园区的游客人数![]() .
.
(2)请问,从12点(即![]() )开始,园区内总人数何时达到最多?并说明理由
)开始,园区内总人数何时达到最多?并说明理由
查看答案和解析>>
科目: 来源: 题型:
【题目】设椭圆![]() 长轴长为4,右焦点
长轴长为4,右焦点![]() 到左顶点的距离为3.
到左顶点的距离为3.
(1)求椭圆![]() 的方程;
的方程;
(2)设过原点![]() 的直线交椭圆于
的直线交椭圆于![]() 两点(
两点(![]() 不在坐标轴上),连接
不在坐标轴上),连接![]() 并延长交椭圆于点
并延长交椭圆于点![]() ,若
,若![]() ,求四边形
,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com