
科目: 来源: 题型:
【题目】体温是人体健康状况的直接反应,一般认为成年人腋下温度T(单位:![]() )平均在
)平均在![]() 之间即为正常体温,超过
之间即为正常体温,超过![]() 即为发热.发热状态下,不同体温可分成以下三种发热类型:低热:
即为发热.发热状态下,不同体温可分成以下三种发热类型:低热:![]() ;高热:
;高热:![]() ;超高热(有生命危险):
;超高热(有生命危险):![]() .某位患者因患肺炎发热,于12日至26日住院治疗.医生根据病情变化,从14日开始,以3天为一个疗程,分别用三种不同的抗生素为该患者进行消炎退热.住院期间,患者每天上午8:00服药,护士每天下午16:00为患者测量腋下体温记录如下:
.某位患者因患肺炎发热,于12日至26日住院治疗.医生根据病情变化,从14日开始,以3天为一个疗程,分别用三种不同的抗生素为该患者进行消炎退热.住院期间,患者每天上午8:00服药,护士每天下午16:00为患者测量腋下体温记录如下:
抗生素使用情况 | 没有使用 | 使用“抗生素A”疗 | 使用“抗生素B”治疗 | |||||
日期 | 12日 | 13日 | 14日 | 15日 | 16日 | 17日 | 18日 | 19日 |
体温( | 38.7 | 39.4 | 39.7 | 40.1 | 39.9 | 39.2 | 38.9 | 39.0 |
抗生素使用情况 | 使用“抗生素C”治疗 | 没有使用 | |||||
日期 | 20日 | 21日 | 22日 | 23日 | 24日 | 25日 | 26日 |
体温( | 38.4 | 38.0 | 37.6 | 37.1 | 36.8 | 36.6 | 36.3 |
(I)请你计算住院期间该患者体温不低于![]() 的各天体温平均值;
的各天体温平均值;
(II)在19日—23日期间,医生会随机选取3天在测量体温的同时为该患者进行某一特殊项目“a项目”的检查,记X为高热体温下做“a项目”检查的天数,试求X的分布列与数学期望;
(III)抗生素治疗一般在服药后2-8个小时就能出现血液浓度的高峰,开始杀灭细菌,达到消炎退热效果.假设三种抗生素治疗效果相互独立,请依据表中数据,判断哪种抗生素治疗效果最佳,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,在直角梯形![]() 中,
中,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的点,
上的点,![]() ,且
,且![]() (如图①).将四边形
(如图①).将四边形![]() 沿
沿![]() 折起,连接
折起,连接![]() 、
、![]() 、
、![]() (如图②).在折起的过程中,则下列表述:
(如图②).在折起的过程中,则下列表述:

①![]() 平面
平面![]() ;
;
②四点![]() 、
、![]() 、
、![]() 、
、![]() 可能共面;
可能共面;
③若![]() ,则平面
,则平面![]() 平面
平面![]() ;
;
④平面![]() 与平面
与平面![]() 可能垂直.其中正确的是__________.
可能垂直.其中正确的是__________.
查看答案和解析>>
科目: 来源: 题型:
【题目】![]() 年初,湖北出现由新型冠状病毒引发的肺炎.为防止病毒蔓延,各级政府相继启动重大突发公共卫生事件一级响应,全国人心抗击疫情.下图表示
年初,湖北出现由新型冠状病毒引发的肺炎.为防止病毒蔓延,各级政府相继启动重大突发公共卫生事件一级响应,全国人心抗击疫情.下图表示![]() 月
月![]() 日至
日至![]() 月
月![]() 日我国新型冠状病毒肺炎单日新增治愈和新增确诊病例数,则下列中表述错误的是( )
日我国新型冠状病毒肺炎单日新增治愈和新增确诊病例数,则下列中表述错误的是( )

A.![]() 月下旬新增确诊人数呈波动下降趋势
月下旬新增确诊人数呈波动下降趋势
B.随着全国医疗救治力度逐渐加大,![]() 月下旬单日治愈人数超过确诊人数
月下旬单日治愈人数超过确诊人数
C.![]() 月
月![]() 日至
日至![]() 月
月![]() 日新增确诊人数波动最大
日新增确诊人数波动最大
D.我国新型冠状病毒肺炎累计确诊人数在![]() 月
月![]() 日左右达到峰值
日左右达到峰值
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,左顶点为
,左顶点为![]() ,且
,且![]() ,
,![]() 是椭圆上一点.
是椭圆上一点.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,直线
两点,直线![]() 别与
别与![]() 轴交于点
轴交于点![]() ,求证:在
,求证:在![]() 轴上存在点
轴上存在点![]() ,使得无论非零实数
,使得无论非零实数![]() 怎样变化,以
怎样变化,以![]() 为直径的圆都必过点
为直径的圆都必过点![]() ,并求出点
,并求出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市为了节约生活用水,计划在本市试行居民生活用水定额管理(即确定一个居民月均用水量标准:用水量不超过![]() 的部分按照平价收费,超过
的部分按照平价收费,超过![]() 的部分按照议价收费).为了较为合理地确定出这个标准,通过抽样获得了40位居民某年的月均用水量(单位:吨),按照分组
的部分按照议价收费).为了较为合理地确定出这个标准,通过抽样获得了40位居民某年的月均用水量(单位:吨),按照分组![]() 制作了频率分布直方图,
制作了频率分布直方图,
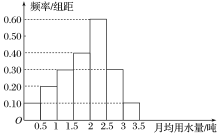
(1)从频率分布直方图中估计该40位居民月均用水量的众数,中位数;
(2)在该样本中月均用水量少于1吨的居民中随机抽取两人,其中两人月均用水量都不低于0.5吨的概率是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】定义:![]() 是无穷数列,若存在正整数k使得对任意
是无穷数列,若存在正整数k使得对任意![]() ,均有
,均有![]() 则称
则称![]() 是近似递增(减)数列,其中k叫近似递增(减)数列
是近似递增(减)数列,其中k叫近似递增(减)数列![]() 的间隔数
的间隔数
(1)若![]() ,
,![]() 是不是近似递增数列,并说明理由
是不是近似递增数列,并说明理由
(2)已知数列![]() 的通项公式为
的通项公式为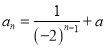 ,其前n项的和为
,其前n项的和为![]() ,若2是近似递增数列
,若2是近似递增数列![]() 的间隔数,求a的取值范围:
的间隔数,求a的取值范围:
(3)已知![]() ,证明
,证明![]() 是近似递减数列,并且4是它的最小间隔数.
是近似递减数列,并且4是它的最小间隔数.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知直线l:![]() 和椭圆
和椭圆![]() :
:![]() 相交于点
相交于点![]() ,
,![]()
(1)当直线l过椭圆![]() 的左焦点和上顶点时,求直线l的方程
的左焦点和上顶点时,求直线l的方程
(2)点![]() 在
在![]() 上,若
上,若![]() ,求
,求![]() 面积的最大值:
面积的最大值:
(3)如果原点O到直线l的距离是![]() ,证明:
,证明:![]() 为直角三角形.
为直角三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com