
科目: 来源: 题型:
【题目】“未来肯定是非接触的,无感支付的方式将成为主流,这有助于降低交互门槛”.云从科技联合创始人姚志强告诉南方日报记者.相对于主流支付方式二维码支付,刷脸支付更加便利,以前出门一部手机解决所有,而现在连手机都不需要了,毕竟,手机支付还需要携带手机,打开二维码也需要时间和手机信号.刷脸支付将会替代手机,成为新的支付方式.某地从大型超市门口随机抽取50名顾客进行了调查,得到了如表列联表:
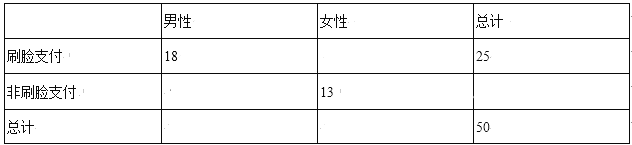
(1)请将上面的列联表补充完整,并判断是否有![]() 的把握认为使用刷脸支付与性别有关?
的把握认为使用刷脸支付与性别有关?
(2)从参加调查且使用刷脸支付的顾客中随机抽取2人参加抽奖活动,抽奖活动规则如下:“一等奖”中奖概率为0.25,奖品为10元购物券![]() 张(
张(![]() ,且
,且![]() ),“二等奖”中奖概率0.25,奖品为10元购物券两张,“三等奖”中奖概率0.5,奖品为10元购物券一张,每位顾客是否中奖相互独立,记参与抽奖的两位顾客中奖购物券金额总和为
),“二等奖”中奖概率0.25,奖品为10元购物券两张,“三等奖”中奖概率0.5,奖品为10元购物券一张,每位顾客是否中奖相互独立,记参与抽奖的两位顾客中奖购物券金额总和为![]() 元,若要使
元,若要使![]() 的均值不低于50元,求
的均值不低于50元,求![]() 的最小值.
的最小值.
附: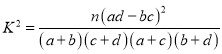 ,其中
,其中![]() .
.

查看答案和解析>>
科目: 来源: 题型:
【题目】在三棱锥,![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点.
的中点.
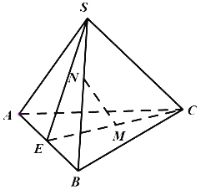
(1)证明:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 平面
平面![]() ?若存在,指出点
?若存在,指出点![]() 的位置并给出证明,若不存在,说明理由;
的位置并给出证明,若不存在,说明理由;
(3)若![]() ,求二面角
,求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目: 来源: 题型:
【题目】新型冠状病毒属于![]() 属的冠状病毒,有包膜,颗粒常为多形性,其中包含着结构为数学模型的
属的冠状病毒,有包膜,颗粒常为多形性,其中包含着结构为数学模型的![]() ,
,![]() ,人体肺部结构中包含
,人体肺部结构中包含![]() ,
,![]() 的结构,新型冠状病毒肺炎是由它们复合而成的,表现为
的结构,新型冠状病毒肺炎是由它们复合而成的,表现为![]() .则下列结论正确的是( )
.则下列结论正确的是( )
A.若![]() ,则
,则![]() 为周期函数
为周期函数
B.对于![]() ,
,![]() 的最小值为
的最小值为![]()
C.若![]() 在区间
在区间![]() 上是增函数,则
上是增函数,则![]()
D.若![]() ,
,![]() ,满足
,满足![]() ,则
,则![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,
,![]() 分别为椭圆C的左、右焦点且
分别为椭圆C的左、右焦点且![]() .
.
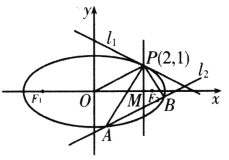
(1)求椭圆C的方程;
(2)过P点的直线![]() 与椭圆C有且只有一个公共点,直线
与椭圆C有且只有一个公共点,直线![]() 平行于OP(O为原点),且与椭圆C交于两点A、B,与直线
平行于OP(O为原点),且与椭圆C交于两点A、B,与直线![]() 交于点M(M介于A、B两点之间).
交于点M(M介于A、B两点之间).
(i)当![]() 面积最大时,求
面积最大时,求![]() 的方程;
的方程;
(ii)求证:![]() ,并判断
,并判断![]() ,
,![]() 的斜率是否可以按某种顺序构成等比数列.
的斜率是否可以按某种顺序构成等比数列.
查看答案和解析>>
科目: 来源: 题型:
【题目】区块链技术被认为是继蒸汽机、电力、互联网之后,下一代颠覆性的核心技术区块链作为构造信任的机器,将可能彻底改变整个人类社会价值传递的方式,2015年至2019年五年期间,中国的区块链企业数量逐年增长,居世界前列现收集我国近5年区块链企业总数量相关数据,如表
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
编号 | 1 | 2 | 3 | 4 | 5 |
企业总数量y(单位:千个) | 2.156 | 3.727 | 8.305 | 24.279 | 36.224 |
注:参考数据![]() (其中z=lny).
(其中z=lny).
附:样本(xi,yi)(i=1,2,…,n)的最小二乘法估计公式为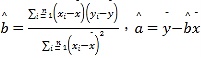
(1)根据表中数据判断,y=a+bx与y=cedx(其中e=2.71828…,为自然对数的底数),哪一个回归方程类型适宜预测未来几年我国区块链企业总数量?(给出结果即可,不必说明理由)
(2)根据(1)的结果,求y关于x的回归方程(结果精确到小数点后第三位);
(3)为了促进公司间的合作与发展,区块链联合总部决定进行一次信息化技术比赛,邀请甲、乙、丙三家区块链公司参赛比赛规则如下:①每场比赛有两个公司参加,并决出胜负;②每场比赛获胜的公司与未参加此场比赛的公司进行下一场的比赛;③在比赛中,若有一个公司首先获胜两场,则本次比赛结束,该公司就获得此次信息化比赛的“优胜公司”,已知在每场比赛中,甲胜乙的概率为![]() ,甲胜丙的概率为
,甲胜丙的概率为![]() ,乙胜丙的概率为
,乙胜丙的概率为![]() ,请通过计算说明,哪两个公司进行首场比赛时,甲公司获得“优胜公司”的概率最大?
,请通过计算说明,哪两个公司进行首场比赛时,甲公司获得“优胜公司”的概率最大?
查看答案和解析>>
科目: 来源: 题型:
【题目】请从下面三个条件中任选一个,补充在下面的横线上,并作答.
①AB⊥BC,②FC与平面ABCD所成的角为![]() ,③∠ABC
,③∠ABC![]() .
.
如图,在四棱锥P﹣ABCD中,底面ABCD是菱形,PA⊥平面ABCD,且PA=AB=2,,PD的中点为F.
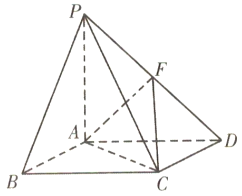
(1)在线段AB上是否存在一点G,使得AF![]() 平面PCG?若存在,指出G在AB上的位置并给以证明;若不存在,请说明理由;
平面PCG?若存在,指出G在AB上的位置并给以证明;若不存在,请说明理由;
(2)若_______,求二面角F﹣AC﹣D的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在四面体ABCD中,△ABC和△BCD均是边长为1的等边三角形,已知四面体ABCD的四个顶点都在同一球面上,且AD是该球的直径,则四面体ABCD的体积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】《周髀算经》是中国古代重要的数学著作,其记载的“日月历法”曰:“阴阳之数,日月之法,十九岁为一章,四章为一部,部七十六岁,二十部为一遂,遂千百五二十岁,….生数皆终,万物复苏,天以更元作纪历”,某老年公寓住有20位老人,他们的年龄(都为正整数)之和恰好为一遂,其中年长者已是奔百之龄(年龄介于90至100),其余19人的年龄依次相差一岁,则年长者的年龄为( )
A.94B.95C.96D.98
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数f(x)为奇函数,且当x≥0时,f(x)=ex﹣cosx,则不等式f(2x﹣1)+f(x﹣2)>0的解集为( )
A.(﹣∞,1)B.(﹣∞,![]() )C.(
)C.(![]() ,+∞)D.(1,+∞)
,+∞)D.(1,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com