
科目: 来源: 题型:
【题目】某植物学家培养出一种观赏性植物,会开出红花或黄花,已知该植物第一代开红花和黄花的概率都是![]() ,从第二代开始,若上一代开红花,则这一代开红花的概率是
,从第二代开始,若上一代开红花,则这一代开红花的概率是![]() ,开黄花的概率是
,开黄花的概率是![]() ;若上一代开黄花,则这一代开红花的概率是
;若上一代开黄花,则这一代开红花的概率是![]() ,开黄花的概率是
,开黄花的概率是![]() .记第n代开红花的概率为
.记第n代开红花的概率为![]() ,第n代开黄花的概率为
,第n代开黄花的概率为![]() .
.
(1)求![]() ;
;
(2)①证明:数列![]() 为等比数列;
为等比数列;
②第![]() 代开哪种颜色花的概率更大?
代开哪种颜色花的概率更大?
查看答案和解析>>
科目: 来源: 题型:
【题目】2020年冬奥会申办成功,让中国冰雪项目迎来了新的发展机会,“十四冬”作为北京冬奥会前重要的练兵场,对冰雪运动产生了不可忽视的带动作用.某校对冰雪体育社团中甲、乙两人的滑轮、雪合战、雪地足球、冰尜(ga)、爬犁速降及俯卧式爬犁6个冬季体育运动项目进行了指标测试(指标值满分为5分,分高者为优),根据测试情况绘制了如图所示的指标雷达图.则下面叙述正确的是( )
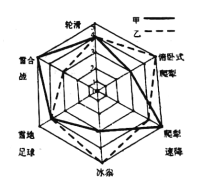
A.甲的轮滑指标高于他的雪地足球指标
B.乙的雪地足球指标低于甲的冰尜指标
C.甲的爬犁速降指标高于乙的爬犁速降指标
D.乙的俯卧式爬犁指标低于甲的雪合战指标
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() ,直线
,直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,
两点,![]() 为坐标原点.
为坐标原点.
(1)若直线![]() 过椭圆
过椭圆![]() 的右焦点
的右焦点![]() ,求
,求![]() 的面积;
的面积;
(2)椭圆![]() 上是否存在点
上是否存在点![]() ,使得四边形
,使得四边形![]() 为平行四边形?若存在,求出所有满足条件的
为平行四边形?若存在,求出所有满足条件的![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】为助力湖北新冠疫情后的经济复苏,某电商平台为某工厂的产品开设直播带货专场.为了对该产品进行合理定价,用不同的单价在平台试销,得到如下数据:
单价 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量 | 90 | 84 | 83 | 80 | 75 | 68 |
(1)根据以上数据,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)若该产品成本是4元/件,假设该产品全部卖出,预测把单价定为多少时,工厂获得最大利润?
(参考公式:回归方程![]() ,其中
,其中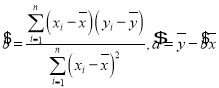 )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】![]() 时代悄然来临,为了研究中国手机市场现状,中国信通院统计了2019年手机市场每月出货量以及与2018年当月同比增长的情况,得到如下统计图,根据该统计图,下列说法错误的是( )
时代悄然来临,为了研究中国手机市场现状,中国信通院统计了2019年手机市场每月出货量以及与2018年当月同比增长的情况,得到如下统计图,根据该统计图,下列说法错误的是( )
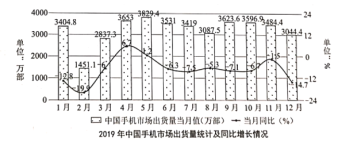
A.2019年全年手机市场出货量中,5月份出货量最多
B.2019年下半年手机市场各月份出货量相对于上半年各月份波动小
C.2019年全年手机市场总出货量低于2018年全年总出货量
D.2018年12月的手机出货量低于当年8月手机出货量
查看答案和解析>>
科目: 来源: 题型:
【题目】一款小游戏的规则如下:每轮游戏要进行三次,每次游戏都需要从装有大小相同的2个红球,3个白球的袋中随机摸出2个球,若摸出的“两个都是红球”出现3次获得200分,若摸出“两个都是红球”出现1次或2次获得20分,若摸出“两个都是红球”出现0次则扣除10分(即获得![]() 分).
分).
(1)设每轮游戏中出现“摸出两个都是红球”的次数为![]() ,求
,求![]() 的分布列;
的分布列;
(2)玩过这款游戏的许多人发现,若干轮游戏后,与最初的分数相比,分数没有增加反而减少了,请运用概率统计的相关知识分析解释上述现象.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com