
科目: 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,离心率是
,离心率是![]() ,P为椭圆上的动点.当
,P为椭圆上的动点.当![]() 取最大值时,
取最大值时,![]() 的面积是
的面积是![]()
(1)求椭圆的方程:
(2)若动直线l与椭圆E交于A,B两点,且恒有![]() ,是否存在一个以原点O为圆心的定圆C,使得动直线l始终与定圆C相切?若存在,求圆C的方程,若不存在,请说明理由
,是否存在一个以原点O为圆心的定圆C,使得动直线l始终与定圆C相切?若存在,求圆C的方程,若不存在,请说明理由
查看答案和解析>>
科目: 来源: 题型:
【题目】在四棱柱![]() 中,已知底面
中,已知底面![]() 为等腰梯形,
为等腰梯形,![]() ,
,![]() ,M,N分别是棱
,M,N分别是棱![]() ,
,![]() 的中点
的中点
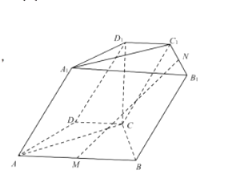
(1)证明:直线![]() 平面
平面![]() ;
;
(2)若![]() 平面
平面![]() ,且
,且![]() ,求经过点A,M,N的平面
,求经过点A,M,N的平面![]() 与平面
与平面![]() 所成二面角的正弦值.
所成二面角的正弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】新生儿某疾病要接种三次疫苗免疫(即0、1、6月龄),假设每次接种之间互不影响,每人每次接种成功的概率相等为了解新生儿该疾病疫苗接种剂量与接种成功之间的关系,现进行了两种接种方案的临床试验:10μg/次剂量组与20μg/次剂量组,试验结果如下:
接种成功 | 接种不成功 | 总计(人) | |
10μg/次剂量组 | 900 | 100 | 1000 |
20μg/次剂量组 | 973 | 27 | 1000 |
总计(人) | 1873 | 127 | 2000 |
(1)根据数据说明哪种方案接种效果好?并判断能否有99.9%的把握认为该疾病疫苗接种成功与两种接种方案有关?
(2)以频率代替概率,若选用接种效果好的方案,参与该试验的1000人的成功人数比此剂量只接种一次的成功人数平均提高多少人.
参考公式: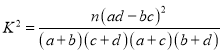 ,其中
,其中![]()
参考附表:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】下面给出有关![]() 的四个论断:①
的四个论断:①![]() ;②
;②![]() ;③
;③![]() 或
或![]() ;④
;④![]() .以其中的三个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:若______,则_______(用序号表示)并给出证明过程:
.以其中的三个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:若______,则_______(用序号表示)并给出证明过程:
查看答案和解析>>
科目: 来源: 题型:
【题目】向体积为1的正方体密闭容器内注入体积为![]() 的液体,旋转容器,下列说法正确的是( )
的液体,旋转容器,下列说法正确的是( )
A.当![]() 时,容器被液面分割而成的两个几何体完全相同
时,容器被液面分割而成的两个几何体完全相同
B.![]() ,液面都可以成正三角形形状
,液面都可以成正三角形形状
C.当液面与正方体的某条体对角线垂直时,液面面积的最大值为![]()
D.当液面恰好经过正方体的某条体对角线时,液面边界周长的最小值为![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知动点![]() 在双曲线
在双曲线![]() 上,双曲线
上,双曲线![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,下列结论正确的是( )
,下列结论正确的是( )
A.![]() 的离心率为
的离心率为![]()
B.![]() 的渐近线方程为
的渐近线方程为![]()
C.动点![]() 到两条渐近线的距离之积为定值
到两条渐近线的距离之积为定值
D.当动点![]() 在双曲线
在双曲线![]() 的左支上时,
的左支上时,![]() 的最大值为
的最大值为![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为:
的参数方程为: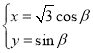 ,(
,(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的非负半轴为极轴建立极坐标系,直线l的极坐标方程为
轴的非负半轴为极轴建立极坐标系,直线l的极坐标方程为![]()
(1)求曲线![]() 和直线l的直角坐标方程;
和直线l的直角坐标方程;
(2)若点![]() 在曲线
在曲线![]() 上,且点
上,且点![]() 到直线l的距离最小,求点
到直线l的距离最小,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]()
![]() 的右焦点为
的右焦点为![]() ,上顶点为
,上顶点为![]() ,
,![]() ,点
,点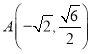 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)动直线l与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() ,与
,与![]() 轴的正半轴相交于点
轴的正半轴相交于点![]() ,
,![]() 为线段
为线段![]() 的中点,若
的中点,若![]() 为定值
为定值![]() ,请判断直线l是否过定点,求实数
,请判断直线l是否过定点,求实数![]() 的值,并说明理由.
的值,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】“扶贫帮困”是中华民族的传统美德,某大型企业为帮扶贫困职工,设立“扶贫帮困基金”,采用如下方式进行一次募捐:在不透明的箱子中放入大小均相同的白球六个,红球三个,每位献爱心的参与者投币100元有一次摸奖机会,一次性从箱中摸球三个(摸完球后将球放回),若有一个红球,奖金20元,两个红球奖金40元,三个全为红球奖金200元.
(1)求一位献爱心参与者不能获奖的概率;
(2)若该次募捐有300位献爱心参与者,求此次募捐所得善款的数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com