
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,
中, ![]() ,动点
,动点![]() 满足:以
满足:以![]() 为直径的圆与
为直径的圆与![]() 轴相切.
轴相切.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,直线
,直线![]() 过点
过点![]() 且与
且与![]() 交于
交于![]() 两点,当
两点,当![]() 与
与![]() 的面积之和取得最小值时,求直线
的面积之和取得最小值时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】从某工厂的一个车间抽取某种产品50件,产品尺寸(单位:cm)落在各个小组的频数分布如下表:
数据分组 | [12.5,15.5) | [15.5,18.5) | [18.5,21.5) | [21.5,24.5) | [24.5,27.5) | [27.5,30.5) | [30.5,33.5) |
频数 | 3 | 8 | 9 | 12 | 10 | 5 | 3 |
(1)根据频数分布表,求该产品尺寸落在[27.5,33.5]内的概率;
(2)求这50件产品尺寸的样本平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(3)根据频数分布对应的直方图,可以认为这种产品尺寸![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为样本平均值
近似为样本平均值![]() ,
,![]() 近似为样本方差
近似为样本方差![]() ,经计算得
,经计算得![]() .利用该正态分布,求
.利用该正态分布,求![]() (
(![]() ).
).
附:(1)若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]()
![]() ;(2)
;(2)![]() .
.
查看答案和解析>>
科目: 来源: 题型:
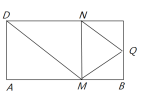
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,点
的中点,点![]() ,
,![]() 分别在线段
分别在线段![]() ,
,![]() 上运动(其中
上运动(其中![]() 不与
不与![]() ,
,![]() 重合,
重合,![]() 不与
不与![]() ,
,![]() 重合),且
重合),且![]() ,沿
,沿![]() 将
将![]() 折起,得到三棱锥
折起,得到三棱锥![]() ,则三棱锥
,则三棱锥![]() 体积的最大值为__________;当三棱锥
体积的最大值为__________;当三棱锥![]() 体积最大时,其外接球的表面积的值为_______________.
体积最大时,其外接球的表面积的值为_______________.
查看答案和解析>>
科目: 来源: 题型:
【题目】古希腊著名数学家阿波罗尼斯与欧几里得、阿基米德齐名.他发现:“平面内到两个定点![]() 的距离之比为定值
的距离之比为定值![]() 的点的轨迹是圆”.后来,人们将这个圆以他的名字命名,称为阿波罗尼斯圆,简称阿氏圆在平面直角坐标系
的点的轨迹是圆”.后来,人们将这个圆以他的名字命名,称为阿波罗尼斯圆,简称阿氏圆在平面直角坐标系![]() 中,
中,![]() 点
点![]() .设点
.设点![]() 的轨迹为
的轨迹为![]() ,下列结论正确的是( )
,下列结论正确的是( )
A. ![]() 的方程为
的方程为![]()
B. 在![]() 轴上存在异于
轴上存在异于![]() 的两定点
的两定点![]() ,使得
,使得![]()
C. 当![]() 三点不共线时,射线
三点不共线时,射线![]() 是
是![]() 的平分线
的平分线
D. 在![]() 上存在点
上存在点![]() ,使得
,使得![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年以来,世界经济和贸易增长放缓,中美经贸摩擦影响持续显现,我国对外贸易仍然表现出很强的韧性.今年以来,商务部会同各省市全面贯彻落实稳外贸决策部署,出台了一系列政策举措,全力营造法治化、国际化、便利化的营商环境,不断提高贸易便利化水平,外贸稳规模、提质量、转动力取得阶段性成效,进出口保持稳中提质的发展势头,下图是某省近五年进出口情况统计图,下列描述正确的是( )
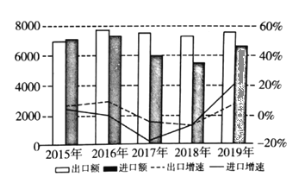
A.这五年,2015年出口额最少B.这五年,出口总额比进口总额多
C.这五年,出口增速前四年逐年下降D.这五年,2019年进口增速最快
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() ,
,![]() 为自然对数的底数.
为自然对数的底数.
(1)若![]() ,求函数
,求函数![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 在定义域上恰有两个不同的零点,求实数a的取值范围;
在定义域上恰有两个不同的零点,求实数a的取值范围;
(3)设函数![]() 在区间
在区间![]() )上存在极值,求证:
)上存在极值,求证:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知正项数列![]() ,
,![]() 满足:对任意正整数
满足:对任意正整数![]() ,都有
,都有![]() ,
,![]() ,
,![]() 成等差数列,
成等差数列,![]() ,
,![]() ,
,![]() 成等比数列,且
成等比数列,且![]() ,
,![]() .
.
(Ⅰ)求证:数列![]() 是等差数列;
是等差数列;
(Ⅱ)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(Ⅲ)设![]() =
=![]() +
+![]() +…+
+…+![]() ,如果对任意的正整数
,如果对任意的正整数![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com