
科目: 来源: 题型:
【题目】《普通高中数学课程标准(2017版)》提出了数学学科的六大核心素养.为了比较甲、乙两名高二学生的数学核心素养水平,现以六大素养为指标对二人进行了测验,根据测验结果绘制了雷达图(如图,每项指标值满分为5分,分值高者为优),则下面叙述正确的是( )
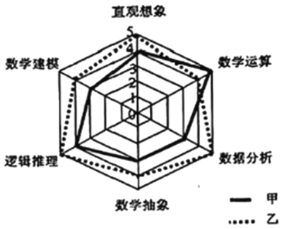
A.甲的数据分析素养高于乙
B.甲的数学建模素养优于数学抽象素养
C.乙的六大素养中逻辑推理最差
D.乙的六大素养整体平均水平优于甲
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年10月,工信部颁发了国内首个![]() 无线电通信设备进网许可证,标志着
无线电通信设备进网许可证,标志着![]() 基站设备将正式接入公用电信商用网络.某
基站设备将正式接入公用电信商用网络.某![]() 手机生产商拟升级设备生产
手机生产商拟升级设备生产![]() 手机,有两种方案可供选择,方案1:直接引进
手机,有两种方案可供选择,方案1:直接引进![]() 手机生产设备;方案2:对已有的
手机生产设备;方案2:对已有的![]() 手机生产设备进行技术改造,升级到
手机生产设备进行技术改造,升级到![]() 手机生产设备.该生产商对未来
手机生产设备.该生产商对未来![]() 手机销售市场行情及回报率进行大数据模拟,得到如下统计表:
手机销售市场行情及回报率进行大数据模拟,得到如下统计表:
市场销售状态 | 畅销 | 平销 | 滞销 | |
市场销售状态概率 |
|
|
| |
预期年利润数值(单位:亿元) | 方案1 | 70 | 40 | -40 |
方案2 | 60 | 30 | -10 | |
(1)以预期年利润的期望值为依据,求![]() 的取值范围,讨论该生产商应该选择哪种方案进行设备升级?
的取值范围,讨论该生产商应该选择哪种方案进行设备升级?
(2)设该生产商升级设备后生产的![]()
![]() 万部,通过大数据模拟核算,选择方案1所生产的
万部,通过大数据模拟核算,选择方案1所生产的![]() 手机年度总成本
手机年度总成本![]() (亿元),选择方案2所生产的
(亿元),选择方案2所生产的![]() 手机年度总成为
手机年度总成为![]() (亿元).已知
(亿元).已知![]() ,当所生产的
,当所生产的![]() 手机市场行情为畅销、平销和滞销时,每部手机销售单价分别为0.8万元,
手机市场行情为畅销、平销和滞销时,每部手机销售单价分别为0.8万元,![]() (万元),
(万元),![]() (万元),根据(1)的决策,求该生产商所生产的
(万元),根据(1)的决策,求该生产商所生产的![]() 手机年利润期望的最大值?并判断这个年利润期望的最大值能否达到预期年利润数值.
手机年利润期望的最大值?并判断这个年利润期望的最大值能否达到预期年利润数值.
查看答案和解析>>
科目: 来源: 题型:
【题目】关于函数![]() ,有下述四个结论:
,有下述四个结论:
①若![]() 在
在![]() 内单调递增,则
内单调递增,则![]() .
.
②若![]() 在
在![]() 内单调递减,则
内单调递减,则![]() .
.
③若![]() 在
在![]() 内有且仅有一个极大值点,则
内有且仅有一个极大值点,则![]() .
.
④若![]() 在
在![]() 内有且仅有一个极小值点,则
内有且仅有一个极小值点,则![]() .
.
其中所有正确结论的序号是( )
A.①③B.②③C.①④D.③④
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,以原点O为极点,x轴的正半轴为极轴建立极坐标系,两种坐标系中取相同的长度单位.已知直线l的参数方程为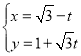 (t为参数),曲线C的极坐标方程为ρ=4sin(θ+
(t为参数),曲线C的极坐标方程为ρ=4sin(θ+![]() ).
).
(1)求直线l的普通方程与曲线C的直角坐标方程;
(2)若直线l与曲线C交于M,N两点,求△MON的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】2018年3月5日上午,李克强总理做政府工作报告时表示,将新能源汽车车辆购置税优惠政策再延长三年,自2018年1月1日至2020年12月31日,对购置的新能源汽车免征车辆购置税.新能源汽车销售的春天来了!从衡阳地区某品牌新能源汽车销售公司了解到,为了帮助品牌迅速占领市场,他们采取了保证公司正常运营的前提下实行薄利多销的营销策略(即销售单价随日销量![]() (台)变化而有所变化),该公司的日盈利
(台)变化而有所变化),该公司的日盈利![]() (万元),经过一段时间的销售得到
(万元),经过一段时间的销售得到![]() ,
,![]() 的一组统计数据如下表:
的一组统计数据如下表:
日销量 | 1 | 2 | 3 | 4 | 5 |
日盈利 | 6 | 13 | 17 | 20 | 22 |
将上述数据制成散点图如图所示:
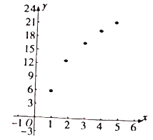
(1)根据散点图判断![]() 与
与![]() 中,哪个模型更适合刻画
中,哪个模型更适合刻画![]() ,
,![]() 之间的关系?并从函数增长趋势方面给出简单的理由;
之间的关系?并从函数增长趋势方面给出简单的理由;
(2)根据你的判断及下面的数据和公式,求出![]() 关于
关于![]() 的回归方程,并预测当日销量
的回归方程,并预测当日销量![]() 时,日盈利是多少?
时,日盈利是多少?
参考公式及数据:线性回归方程![]() ,其中
,其中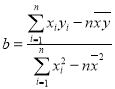 ,
,![]() ;
;
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com