【题目】如图，在四棱锥中，平面平面，是的中点，是上一点，且

（1）求证:平面；

（2）若求直线与平面所成角的正弦值.

【题目】设函数，.

（1）求函数的图象在处的切线方程；

（2）求证：方程有两个实数根；

（3）求证：.

【题目】如图，四棱锥中，侧面底面，，，，，，分别为的中点.

（1）求证：平面；

（2）求二面角的余弦值；

（3）在线段上是否存在一点，使与平面所成角的正弦值为，若存在求出的长，若不存在说明理由.

（1）设表示上午抽到的社区工作者的人数，求随机变量的分布列和数学期望；

（2）设为事件“全天抽到的名工作人员的身份互不相同”，求事件发生的概率.

【题目】已知，函数

（1）若在上单调递增，则的取值范围为______________；

（2）若对于任意实数，方程有且只有一个实数根，且，函数的图象与函数的图象有三个不同的交点，则的取值范围为______________.

【题目】在平面直角坐标系xOy中，曲线C1的参数方程为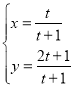（t为参数），曲线C2的参数方程为（α为参数），以坐标原点为极点.x轴正半轴为极轴建立极坐标系.

（Ⅰ）求曲线C1的普通方程和曲线C2的极坐标方程；

（Ⅱ）射线与曲线C2交于O，P两点，射线与曲线C1交于点Q，若△OPQ的面积为1，求|OP|的值.

【题目】已知函数.

（Ⅰ）若函数有两个零点，求a的取值范围；

（Ⅱ）恒成立，求a的取值范围.

根据行业质量标准规定，该核心部件尺寸x满足：|x﹣12|≤1为一级品，1＜|x﹣12|≤2为二级品，|x﹣12|＞2为三级品.

（Ⅰ）现根据频率分布直方图中的分组，用分层抽样的方法先从这400件样本中抽取40件产品，再从所抽取的40件产品中，抽取2件尺寸x∈[12，15]的产品，记ξ为这2件产品中尺寸x∈[14，15]的产品个数，求ξ的分布列和数学期望；

（Ⅱ）将甲设备生产的产品成箱包装出售时，需要进行检验.已知每箱有100件产品，每件产品的检验费用为50元.检验规定：若检验出三级品需更换为一级或二级品；若不检验，让三级品进入买家，厂家需向买家每件支付200元补偿.现从一箱产品中随机抽检了10件，结果发现有1件三级品.若将甲设备的样本频率作为总体的慨率，以厂家支付费用作为决策依据，问是否对该箱中剩余产品进行一一检验？请说明理由；

（Ⅲ）为加大升级力度，厂家需增购设备.已知这种产品的利润如下：一级品的利润为500元/件；二级品的利润为400元/件；三级品的利润为200元/件.乙种设备产品中一、二、三级品的概率分别是，，.若将甲设备的样本频率作为总体的概率，以厂家的利润作为决策依据.应选购哪种设备？请说明理由.

【题目】已知F1，F2是椭圆C：（a＞b＞0）的左、右焦点，过椭圆的上顶点的直线x+y=1被椭圆截得的弦的中点坐标为.

（Ⅰ）求椭圆C的方程；

（Ⅱ）过F1的直线l交椭圆于A，B两点，当△ABF2面积最大时，求直线l的方程.

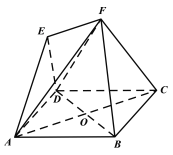
（Ⅰ）求证：BD⊥平面ACF；

（Ⅱ）求平面DEF与平面ABCD所成角的正弦值.