【题目】以直角坐标系的原点为极点，轴的正半轴为极轴，两个坐标系取相等的长度单位.已知圆的参数方程为（为参数），直线的直角坐标方程为.

（1）求圆的普通方程和直线的极坐标方程；

（2）设圆和直线交于两点，求的面积.

【题目】已知函数（自然对数的底数）有两个零点.

（1）求实数的取值范围；

（2）若的两个零点分别为，证明：.

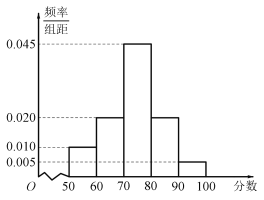
（1）估计这100位学生的数学成绩的平均值.（同一组中的数据用该组区间的中点值代表）；

（2）根据整个年级的数学成绩，可以认为学生的数学成绩近似地服从正态分布经计算，（1）问中样本标准差的近似值为10．用样本平均数作为的近似值，用样本标准差作为的估计值，现任抽取一位学生，求他的数学成绩恰在64分到94分之间的概率.

参考数据:若随机变量，则，，

（3）该年级1班的数学老师为了能每天督促学生的网络学习，提高学生每天的作业质量及学习数学的积极性，特意在微信上设计了一个每日作业小程序，每当学生提交的作业获得优秀时，就有机会参与一次小程序中“玩游戏，得奖励积分”的活动，开学后可根据获得积分的多少领取老师相应的小奖品.小程序页面上有一列方格，共15格，刚开始有只小兔子在第1格，每点一下游戏的开始按钮，小兔子就沿着方格跳一下，每次跳1格或跳2格，概率均为，依次点击游戏的开始按钮，直到小兔子跳到第14格（奖励0分）或第15格（奖励5分）时，游戏结束，每天的积分自动累加，设小兔子跳到第格的概率为，试证明是等比数列，并求的值.（获胜的概率）

【题目】已知抛物线：的焦点为，直线：与抛物线交于，两点.

（1）若，求直线的方程；

（2）过点作直线交抛物线于，两点，若线段，的中点分别为，，直线与轴的交点为，求点到直线与距离和的最大值.

【题目】已知四边形是梯形，如图，，，，为的中点，以为折痕把折起，使点到达点的位置（如图2），且

（1）求证：平面平面；

（2）求与平面所成角的正弦值.

【题目】对于函数（为自然对数的底数，），函数，给出下列结论：

①函数的图象在处的切线在轴的截距为

②函数是奇函数，且在上单调递增；

③函数存在唯一的极小值点，其中，且；

④函数存在两个极小值点，和两个极大值点，且.

其中所有正确结论的序号是（ ）

A.①②③B.①④C.①③④D.②④

A.4万元B.5.5万元C.6.5万元D.10万元

A.B.C.D.

【题目】已知函数.

（1）讨论的单调性.

（2）试问是否存在，使得对恒成立？若存在，求的取值范围；若不存在，请说明理由.

【题目】已知椭圆的长轴长为，焦距为2，抛物线的准线经过C的左焦点F.

（1）求C与M的方程；

（2）直线l经过C的上顶点且l与M交于P，Q两点，直线FP，FQ与M分别交于点D（异于点P），E（异于点Q），证明:直线DE的斜率为定值.