
科目: 来源: 题型:
【题目】如图,一颗棋子从三棱柱的一个项点沿棱移到相邻的另一个顶点的概率均为![]() ,刚开始时,棋子在上底面点
,刚开始时,棋子在上底面点![]() 处,若移了
处,若移了![]() 次后,棋子落在上底面顶点的概率记为
次后,棋子落在上底面顶点的概率记为![]() .
.
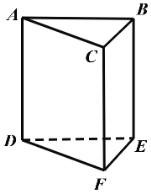
(1)求![]() ,
,![]() 的值:
的值:
(2)求证:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,求实数
,求实数![]() ,
,![]() 的值:
的值:
(2)求证:当![]() 时,
时,![]() 在
在![]() 上有两个极值点:
上有两个极值点:
(3)设![]() ,若
,若![]() 在
在![]() 单调递减,求实数
单调递减,求实数![]() 的取值范围.(其中
的取值范围.(其中![]() 为自然对数的底数)
为自然对数的底数)
查看答案和解析>>
科目: 来源: 题型:
【题目】给定数列![]() ,记该数列前
,记该数列前![]() 项
项![]() 中的最大项为
中的最大项为![]() ,该数列后
,该数列后![]() 项
项![]() ,
,![]() , …..,
, …..,![]() 中的最小项为
中的最小项为![]() ,
,![]() .
.
(1)对于数列:3,4,7,1,求出相应的![]() ,
,![]() ,
,![]() ;
;
(2)![]() 是数列
是数列![]() 的前
的前![]() 项和,若对任意
项和,若对任意![]() ,有
,有![]() ,其中
,其中![]() 且
且![]() ,
,
①设![]() ,判断数列
,判断数列![]() 是否为等比数列;
是否为等比数列;
②若数列![]() 对应的
对应的![]() 满足:
满足:![]() 对任意的正整数
对任意的正整数![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】某杂肉观赏区改造建筑用地平面示意图如图所示、经规划调研确定,杂肉观赏区改造规划建筑用地区域是半径为![]() 的圆,该圆面的内接四边形
的圆,该圆面的内接四边形![]() 是原杂肉观赏区建筑用地,测量可知边界
是原杂肉观赏区建筑用地,测量可知边界![]() 千米,
千米,![]() 千米,
千米,![]() 千米.
千米.
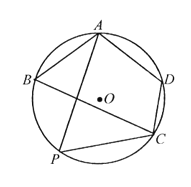
(1)请计算原杂肉观赏区建筑用地![]() 的面积及圆面的半径
的面积及圆面的半径![]() 的值;
的值;
(2)因地理条件的限制,边界![]() 、
、![]() 不能变更,而边界
不能变更,而边界![]() 、
、![]() 可以调整,为了提高杂肉观赏区观赏的时长,请在圆弧
可以调整,为了提高杂肉观赏区观赏的时长,请在圆弧![]() 上设计一点
上设计一点![]() ,使得杂肉观赏区改造的新建筑用地
,使得杂肉观赏区改造的新建筑用地![]() 的周长最大,并求最大值.
的周长最大,并求最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过右焦点F的直线L与C相交于A、B两点,当L的斜率为1时,坐标原点O到L的距离为
,过右焦点F的直线L与C相交于A、B两点,当L的斜率为1时,坐标原点O到L的距离为![]() .
.
(1)求椭圆的标准方程;
(2)在C上是否存在点P,使得当L绕F转到某一位置时,有![]() 成立?若存在,求出所有的P的坐标与L的方程;若不存在,说明理由.
成立?若存在,求出所有的P的坐标与L的方程;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线C的顶点是原点O,以x轴为对称轴,且经过点P(1,2).
(1)求抛物线C的方程;
设点A,B在抛物线C上,直线PA,PB分别与y轴交于点M,N,|PM|=|PN|.求直线AB的斜率.
查看答案和解析>>
科目: 来源: 题型:
【题目】某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量(单位:克)分别在[100,150),[150,200),[200,250),[250,300),[300,350),[350,400]中,经统计得频率分布直方图如图所示.
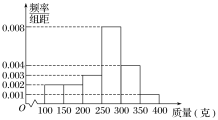
(1)现按分层抽样的方法从质量为[250,300),[300,350)内的芒果中随机抽取6个,再从这6个中随机抽取3个,求这3个芒果中恰有1个在[300,350)内的概率;
(2)某经销商来收购芒果,以各组数据的中间数代表这组数据的平均值,用样本估计总体,该种植园中还未摘下的芒果大约还有10 000个,经销商提出如下两种收购方案:A方案:所有芒果以10元/千克收购;B方案:对质量低于250克的芒果以2元/个收购,高于或等于250克的以3元/个收购.通过计算确定种植园选择哪种方案获利更多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com