【题目】在平面直角坐标系中，曲线的参数方程为（为参数），直线经过点且倾斜角为，，以原点为极点，轴的正半轴为极轴建立极坐标系.

（1）求曲线的极坐标方程；

（2）过原点作直线的垂线，垂足为，交曲线于另一点，当变化时，求的面积的最大值及相应的的值.

【题目】已知函数.

（1）若是函数的极值点，求a的值；

（2）当时，证明：.

【题目】已知椭圆，将其左、右焦点和短轴的两个端点顺次连接得到一个面积为的正方形.

（1）求椭圆的方程；

（2）直线与椭圆交于、两点（均不在轴上），点，若直线、、的斜率成等比数列，且的面积为（为坐标原点），求直线的方程.

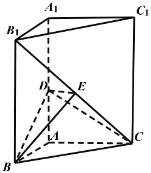
（1）证明：DE⊥平面BCC1B1；

（2）若直线BE与平面AA1B1B所成角为30°，求二面角C﹣BD﹣E的大小.

假设学生甲每次考试各题的得分相互独立.

（1）若此项竞赛考试四道题的顺序依次为代数、几何、数论、组合，试预测学生甲考试得160分的概率；

（2）学生甲研究该项竞赛近五年的试题发现第1题都是代数题，于是他在赛前针对代数版块进行了强化训练，并取得了很大进步，现在，只要代数题是在试卷第1、2题的位置，他就一定能答对，若今年该项数学竞赛考试四道题的顺序依次为代数、数论、组合、几何，试求学生甲此次考试得分X的分布列.

（1）求{an}的通项公式；

（2）若数列{bn}满足b1＝0，bn+1﹣bn＝1，设cn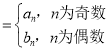，求数列{cn}的前2n项和.

【题目】已知四点均在函数f（x）＝log2的图象上，若四边形ABCD为平行四边形，则四边形ABCD的面积是（ ）

A.B.C.D.

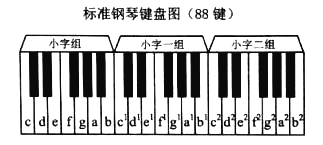
【题目】音乐是用声音来表达人的思想感情的一种艺术，明代的律学家朱载堉创建了十二平均律，并把十二平均律计算得十分精确，与当今的十二平均律完全相同，其方法是将一个八度音程（即相邻的两个具有相同名称的音之间，如图中88键标准钢琴键盘的一部分中，c到c1便是一个八度音程）均分为十二等分的音律，如果用正式的音乐术语称呼原来的7个音符，分别是c，d，e，f，g，a，b，则多出来的5个音符为c#（读做“升c”），d#，f#，g#，a#；12音阶为：c，c#，d，d#，e，f，f#，g，g#，a，a#，b，相邻音阶的频率之比为1：.如图，则键盘c和d的频率之比为即1：，键盘e和f的频率之比为1：，键盘c和c1的频率之比为1：2，由此可知，图中的键盘b1和f2的频率之比为（ ）

A.B.1：C.：1D.：1

A.lα，mβ，l∥mB.l⊥m，l∥α，m⊥β

C.lα，mα，l∥β，m∥βD.l∥m，l⊥α，m⊥β

【题目】在平面直角坐标系中，曲线C的参数方程为（为参数，）.以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，直线l的圾坐标方，且直线l与曲线C相交于A，B两点.

（1）求曲线C的普通方程和l的直角坐标方程；

（2）若，点满足，求此时r的值.