
科目: 来源: 题型:
【题目】厂家在产品出厂前,需对产品做检验,厂家将一批产品发给商家时,商家按合同规定也需随机抽取一定数量的产品做检验,以决定是否接收这批产品.
(1)若厂家库房中(视为数量足够多)的每件产品合格的概率为 ![]() 从中任意取出 3件进行检验,求至少有
从中任意取出 3件进行检验,求至少有![]() 件是合格品的概率;
件是合格品的概率;
(2)若厂家发给商家![]() 件产品,其中有
件产品,其中有![]() 不合格,按合同规定 商家从这
不合格,按合同规定 商家从这![]() 件产品中任取
件产品中任取![]() 件,都进行检验,只有
件,都进行检验,只有![]() 件都合格时才接收这批产品,否则拒收.求该商家可能检验出的不合格产品的件数ξ的分布列,并求该商家拒收这批产品的概率.
件都合格时才接收这批产品,否则拒收.求该商家可能检验出的不合格产品的件数ξ的分布列,并求该商家拒收这批产品的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C的参数方程为![]() ,(θ为参数),以原点为极点,x轴非负半轴为极轴建立极坐标系.
,(θ为参数),以原点为极点,x轴非负半轴为极轴建立极坐标系.
(1)求曲线C的极坐标方程;
(2)在平面直角坐标系xOy中,A(﹣2,0),B(0,﹣2),M是曲线C上任意一点,求△ABM面积的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() ,
,![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 图象在
图象在![]() 处的切线方程;
处的切线方程;
(2)若对任意![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(3)若![]() 存在极大值和极小值,且极大值小于极小值,求
存在极大值和极小值,且极大值小于极小值,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() (
(![]() )上的两个动点
)上的两个动点![]() 和
和![]() ,焦点为F.线段AB的中点为
,焦点为F.线段AB的中点为![]() ,且A,B两点到抛物线的焦点F的距离之和为8.
,且A,B两点到抛物线的焦点F的距离之和为8.
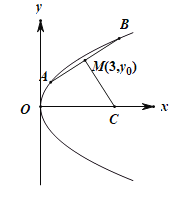
(1)求抛物线的标准方程;
(2)若线段AB的垂直平分线与x轴交于点C,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】等比数列{an}的各项均为正数,且2a1+3a2=1, ![]() =9a2a6.
=9a2a6.
(1)求数列{an}的通项公式;
(2)设bn=log3a1+log3a2+…+log3an,求数列![]() 的前n项和.
的前n项和.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知在![]() 上任意一点
上任意一点![]() 处的切线
处的切线![]() 为
为![]() ,若过右焦点
,若过右焦点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,已知在点
两点,已知在点![]() 处切线相交于
处切线相交于![]() .
.
(Ⅰ)求![]() 点的轨迹方程;
点的轨迹方程;
(Ⅱ)①若过点![]() 且与直线
且与直线![]() 垂直的直线(斜率存在且不为零)交椭圆
垂直的直线(斜率存在且不为零)交椭圆![]() 于
于![]() 两点,证明
两点,证明![]() 为定值.
为定值.
②四边形![]() 的面积是否有最小值,若有请求出最小值;若没有请说明理由.
的面积是否有最小值,若有请求出最小值;若没有请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() ).
).
(1)若![]() ,且
,且![]() 在
在![]() 内有且只有一个零点,求
内有且只有一个零点,求![]() 的值;
的值;
(2)若![]() ,且
,且![]() 有三个不同零点,问是否存在实数
有三个不同零点,问是否存在实数![]() 使得这三个零点成等差数列?若存在,求出
使得这三个零点成等差数列?若存在,求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】![]() 指数是用体重公斤数除以身高米数的平方得出的数字,是国际上常用的衡量人体胖瘦程度以及是否健康的一个标准.对于高中男体育特长生而言,当
指数是用体重公斤数除以身高米数的平方得出的数字,是国际上常用的衡量人体胖瘦程度以及是否健康的一个标准.对于高中男体育特长生而言,当![]() 数值大于或等于20.5时,我们说体重较重,当
数值大于或等于20.5时,我们说体重较重,当![]() 数值小于20.5时,我们说体重较轻,身高大于或等于
数值小于20.5时,我们说体重较轻,身高大于或等于![]() 我们说身高较高,身高小于170cm我们说身高较矮.
我们说身高较高,身高小于170cm我们说身高较矮.
(Ⅰ)已知某高中共有32名男体育特长生,其身高与![]() 指数的数据如散点图,请根据所得信息,完成下述列联表,并判断是否有
指数的数据如散点图,请根据所得信息,完成下述列联表,并判断是否有![]() 的把握认为男生的身高对
的把握认为男生的身高对![]() 指数有影响.
指数有影响.

身高较矮 | 身高较高 | 合计 | |
体重较轻 | |||
体重较重 | |||
合计 |
(Ⅱ)①从上述32名男体育特长生中随机选取8名,其身高和体重的数据如表所示:
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
身高 | 166 | 167 | 160 | 173 | 178 | 169 | 158 | 173 |
体重 | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
根据最小二乘法的思想与公式求得线性回归方程为![]() .利用已经求得的线性回归方程,请完善下列残差表,并求
.利用已经求得的线性回归方程,请完善下列残差表,并求![]() (解释变量(身高)对于预报变量(体重)变化的贡献值)(保留两位有效数字);
(解释变量(身高)对于预报变量(体重)变化的贡献值)(保留两位有效数字);
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
体重(kg) | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
残差 |
|
|
|
|
|
|
|
②通过残差分析,对于残差的最大(绝对值)的那组数据,需要确认在样本点的采集中是否有人为的错误,已知通过重新采集发现,该组数据的体重应该为![]() .小明重新根据最小二乘法的思想与公式,已算出
.小明重新根据最小二乘法的思想与公式,已算出![]() ,请在小明所算的基础上求出男体育特长生的身高与体重的线性回归方程.
,请在小明所算的基础上求出男体育特长生的身高与体重的线性回归方程.
参考数据:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
参考公式: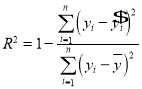 ,
,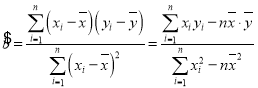 ,
,![]() ,
,![]() ,
,![]() .
.
| 0.10 | 0.05 | 0.01 | 0.005 |
| 2.706 | 3.811 | 6.635 | 7.879 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com