
科目: 来源: 题型:
【题目】在平面直角坐标系中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]()
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() ,点
,点![]() 为曲线
为曲线![]() 上的动点,求线段
上的动点,求线段![]() 的中点
的中点![]() 到直线
到直线![]() 的距离的最大值.并求此时点
的距离的最大值.并求此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】某地为鼓励群众参与“全民读书活动”,增加参与读书的趣味性.主办方设计这样一个小游戏:参与者抛掷一枚质地均匀的骰子(正方体,六个面上分别标注1,2,3,4,5,6六个数字).若朝上的点数为偶数.则继续抛掷一次.若朝上的点数为奇数,则停止游戏,照这样的规则进行,最多允许抛掷3次.每位参与者只能参加一次游戏.
(1)求游戏结束时朝上点数之和为5的概率;
(2)参与者可以选择两种方案:方案一:游戏结束时,若朝上的点数之和为偶数,奖励3本不同的畅销书;若朝上的点数之和为奇数,奖励1本畅销书.方案二:游戏结束时,最后一次朝上的点数为偶数,奖励5本不同的畅销书,否则,无奖励.试分析哪一种方案能使游戏参与者获得更多畅销书奖励?并说明判断的理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知平面内动点![]() 与点
与点![]() ,
,![]() 连线的斜率之积为
连线的斜率之积为![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() ,
,![]() 两点,直线
两点,直线![]() ,
,![]() 与直线
与直线![]() 分别交于
分别交于![]() ,
,![]() 两点.求证:以
两点.求证:以![]() 为直径的圆恒过定点.
为直径的圆恒过定点.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,曲线![]() 的参数方程为
的参数方程为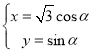 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]()
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() ,点
,点![]() 为曲线
为曲线![]() 上的动点,求线段
上的动点,求线段![]() 的中点
的中点![]() 到直线
到直线![]() 的距离的最大值.并求此时点
的距离的最大值.并求此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】随着生活水平的逐步提高,人们对文娱活动的需求与日俱增,其中观看电视就是一种老少皆宜的娱乐活动.但是我们在观看电视娱乐身心的同时,也要注意把握好观看时间,近期研究显示,一项久坐的生活指标——看电视时间,是导致视力下降的重要因素,即看电视时间越长,视力下降的风险越大.研究者在某小区统计了每天看电视时间![]() (单位:小时)与视力下降人数
(单位:小时)与视力下降人数![]() 的相关数据如下:
的相关数据如下:
编号 | 1 | 2 | 3 | 4 | 5 |
| 1 | 1.5 | 2 | 2.5 | 3 |
| 12 | 16 | 22 | 24 | 26 |
(1)请根据上面的数据求![]() 关于
关于![]() 的线性回归方程
的线性回归方程
(2)我们用(1)问求出的线性回归方程![]() 的
的![]() 估计回归方程
估计回归方程![]() ,由于随机误差
,由于随机误差![]() ,所以
,所以![]() 是
是![]() 的估计值,
的估计值,![]() 成为点(
成为点(![]() ,
,![]() )的残差.
)的残差.
①填写下面的残差表,并绘制残差图;
编号 | 1 | 2 | 3 | 4 | 5 |
| 1 | 1.5 | 2 | 2.5 | 3 |
| 12 | 16 | 22 | 24 | 26 |
|
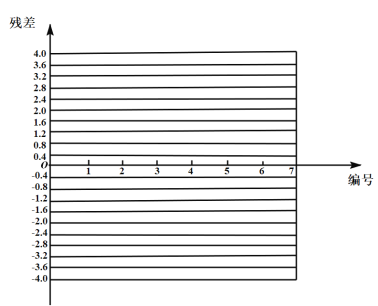
②若残差图所在带状区域宽度不超过4,我们则认为该模型拟合精度比较高,回归方程的预报精度较高,试根据①绘制的残差图分折该模型拟合精度是否比较高?
附:回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为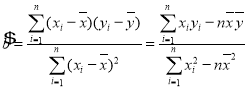 ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援,现对已选出的一组玉米的茎高进行统计,获得茎叶图如图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.

(1)求出易倒伏玉米茎高的中位数![]() ;
;
(2)根据茎叶图的数据,完成下面的列联表:
抗倒伏 | 易倒伏 | |
矮茎 | ||
高茎 |
(3)根据(2)中的列联表,是否可以在犯错误的概率不超过1%的前提下,认为抗倒伏与玉米矮茎有关?
附: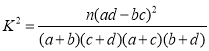 ,
,
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】![]() 网络是一种先进的高频传输技术,我国的
网络是一种先进的高频传输技术,我国的![]() 技术发展迅速,已位居世界前列.华为公司2019年8月初推出了一款
技术发展迅速,已位居世界前列.华为公司2019年8月初推出了一款![]() 手机,现调查得到该款
手机,现调查得到该款![]() 手机上市时间
手机上市时间![]() 和市场占有率
和市场占有率![]() (单位:%)的几组相关对应数据.如图所示的折线图中,横轴1代表2019年8月,2代表2019年9月……,5代表2019年12月,根据数据得出
(单位:%)的几组相关对应数据.如图所示的折线图中,横轴1代表2019年8月,2代表2019年9月……,5代表2019年12月,根据数据得出![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() .若用此方程分析并预测该款手机市场占有率的变化趋势,则最早何时该款
.若用此方程分析并预测该款手机市场占有率的变化趋势,则最早何时该款![]() 手机市场占有率能超过0.5%(精确到月)( )
手机市场占有率能超过0.5%(精确到月)( )

A.2020年6月B.2020年7月C.2020年8月D.2020年9月
查看答案和解析>>
科目: 来源: 题型:
【题目】在①![]() ,且
,且![]() ,②
,②![]() ,且
,且![]() ,③
,③![]() ,且
,且![]() 这三个条件中任选一个,补充在下面问题中,若问题中的
这三个条件中任选一个,补充在下面问题中,若问题中的![]() 存在,求出
存在,求出![]() 和数列
和数列![]() 的通项公式与前
的通项公式与前![]() 项和;若
项和;若![]() 不存在,请说明理由.
不存在,请说明理由.
设![]() 为各项均为正数的数列
为各项均为正数的数列![]() 的前
的前![]() 项和,满足________,是否存在
项和,满足________,是否存在![]() ,使得数列
,使得数列![]() 成为等差数列?
成为等差数列?
查看答案和解析>>
科目: 来源: 题型:
【题目】2020年寒假是特殊的寒假,因为疫情全体学生只能在家进行网上在线学习,为研究学生网上学习的情况,某校社团对男女各10名学生进行了网上在线学习的问卷调查,每名学生给出评分(满分100分),得到如图所示的茎叶图.
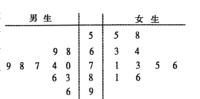
(1)根据茎叶图判断男生组和女生组哪个组对网课的评价更高?并说明理由;
(2)如图是按该20名学生的评分绘制的频率分布直方图,求![]() 的值并估计这20名学生评分的平均值(同一组中的数据用该组区间中点值作为代表);
的值并估计这20名学生评分的平均值(同一组中的数据用该组区间中点值作为代表);
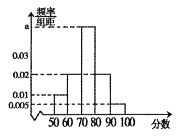
(3)求该20名学生评分的中位数![]() ,并将评分超过
,并将评分超过![]() 和不超过
和不超过![]() 的学生数填入下面的列联表:
的学生数填入下面的列联表:
超过 | 不超过 | |
男生 | ||
女生 |
根据列联表,能否有![]() 的把握认为男生和女生的评分有差异?
的把握认为男生和女生的评分有差异?
附: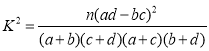 ,
,
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com