
科目: 来源: 题型:
【题目】某农场更新技术培育了一批新型的“盆栽果树”,这种“盆栽果树”将一改陆地栽植果树只在秋季结果的特性,能够一年四季都有花、四季都结果.现为了了解果树的结果情况,从该批果树中随机抽取了容量为120的样本,测量这些果树的高度(单位:厘米),经统计将所有数据分组后得到如图所示的频率分布直方图.
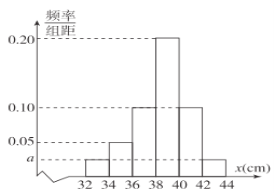
(1)求![]() ;
;
(2)已知所抽取的样本来自![]() 两个实验基地,规定高度不低于40厘米的果树为“优品盆栽”,
两个实验基地,规定高度不低于40厘米的果树为“优品盆栽”,
(i)请将图中列联表补充完整,并判断是否有![]() 的把握认为“优品盆栽”与
的把握认为“优品盆栽”与![]() 两个实验基地有关?
两个实验基地有关?
优品 | 非优品 | 合计 | |
| 60 | ||
| 20 | ||
合计 |
(ii)用样本数据来估计这批果树的生长情况,若从该农场培育的这批“盆栽果树”中随机抽取4棵,求其中“优品盆栽”的棵树![]() 的分布列和数学期望.
的分布列和数学期望.
附:
|
|
|
|
|
|
|
|
![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,
,![]() ,设
,设![]() ,
,![]() .
.
(Ⅰ)求证:数列![]() 是等比数列;
是等比数列;
(Ⅱ)若![]() ,
,![]() ,求实数
,求实数![]() 的最小值;
的最小值;
(Ⅲ)当![]() 时,给出一个新数列
时,给出一个新数列![]() ,其中
,其中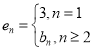 ,设这个新数列的前
,设这个新数列的前![]() 项和为
项和为![]() ,若
,若![]() 可以写成
可以写成![]() (
(![]() ,
,![]() 且
且![]() ,
,![]() )的形式,则称
)的形式,则称![]() 为“指数型和”.问
为“指数型和”.问![]() 中的项是否存在“指数型和”,若存在,求出所有“指数型和”;若不存在,请说明理由.
中的项是否存在“指数型和”,若存在,求出所有“指数型和”;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆C:![]() 经过定点
经过定点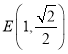 ,其左右集点分别为
,其左右集点分别为![]() ,
,![]() 且
且![]() ,过右焦
,过右焦![]() 且与坐标轴不垂直的直线l与椭圈交于P,Q两点.
且与坐标轴不垂直的直线l与椭圈交于P,Q两点.
(1)求椭圆C的方程:
(2)若O为坐标原点,在线段![]() 上是否存在点
上是否存在点![]() ,使得以
,使得以![]() ,
,![]() 为邻边的平行四边形是菱形?若存在,求出m的取值范围;若不存在,请说明理由.
为邻边的平行四边形是菱形?若存在,求出m的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,某街道居委会拟在![]() 地段的居民楼正南方向的空白地段
地段的居民楼正南方向的空白地段![]() 上建一个活动中心,其中
上建一个活动中心,其中![]() 米.活动中心东西走向,与居民楼平行. 从东向西看活动中心的截面图的下部分是长方形
米.活动中心东西走向,与居民楼平行. 从东向西看活动中心的截面图的下部分是长方形![]() ,上部分是以
,上部分是以![]() 为直径的半圆. 为了保证居民楼住户的采光要求,活动中心在与半圆相切的太阳光线照射下落在居民楼上的影长
为直径的半圆. 为了保证居民楼住户的采光要求,活动中心在与半圆相切的太阳光线照射下落在居民楼上的影长![]() 不超过
不超过![]() 米,其中该太阳光线与水平线的夹角
米,其中该太阳光线与水平线的夹角![]() 满足
满足![]() .
.

(1)若设计![]() 米,
米,![]() 米,问能否保证上述采光要求?
米,问能否保证上述采光要求?
(2)在保证上述采光要求的前提下,如何设计![]() 与
与![]() 的长度,可使得活动中心的截面面积最大?(注:计算中
的长度,可使得活动中心的截面面积最大?(注:计算中![]() 取3)
取3)
查看答案和解析>>
科目: 来源: 题型:
【题目】正四棱锥![]() 的底面正方形边长是3,
的底面正方形边长是3,![]() 是在底面上的射影,
是在底面上的射影,![]() ,
,![]() 是
是![]() 上的一点,过
上的一点,过![]() 且与
且与![]() 、
、![]() 都平行的截面为五边形
都平行的截面为五边形![]() .
.
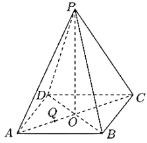
(1)在图中作出截面![]() ,并写出作图过程;
,并写出作图过程;
(2)求该截面面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】向量集合![]() ,对于任意
,对于任意![]() ,以及任意
,以及任意![]() ,都有
,都有![]() ,则称
,则称![]() 为“
为“![]() 类集”,现有四个命题:
类集”,现有四个命题:
①若![]() 为“
为“![]() 类集”,则集合
类集”,则集合![]() 也是“
也是“![]() 类集”;
类集”;
②若![]() ,
,![]() 都是“
都是“![]() 类集”,则集合
类集”,则集合![]() 也是“
也是“![]() 类集”;
类集”;
③若![]() 都是“
都是“![]() 类集”,则
类集”,则![]() 也是“
也是“![]() 类集”;
类集”;
④若![]() 都是“
都是“![]() 类集”,且交集非空,则
类集”,且交集非空,则![]() 也是“
也是“![]() 类集”.
类集”.
其中正确的命题有________(填所有正确命题的序号)
查看答案和解析>>
科目: 来源: 题型:
【题目】以直角坐标系![]() 的原点为极点,x轴的非负半轴为极轴建立极坐标系,并且在两种坐标系中取相同的长度单位.若将曲线
的原点为极点,x轴的非负半轴为极轴建立极坐标系,并且在两种坐标系中取相同的长度单位.若将曲线![]() (
(![]() 为参数)上每一点的横坐标变为原来的
为参数)上每一点的横坐标变为原来的![]() (纵坐标不变),然后将所得图象向右平移2个单位,再向上平移3个单位得到曲线C.直线l的极坐标方程为
(纵坐标不变),然后将所得图象向右平移2个单位,再向上平移3个单位得到曲线C.直线l的极坐标方程为![]() .
.
(1)求曲线C的普通方程;
(2)设直线l与曲线C交于A,B两点,与x轴交于点P,线段AB的中点为M,求![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的中心在原点,左焦点
的中心在原点,左焦点![]() 、右焦点
、右焦点![]() 都在
都在![]() 轴上,点
轴上,点![]() 是椭圆
是椭圆![]() 上的动点,
上的动点,![]() 的面积的最大值为
的面积的最大值为![]() ,在
,在![]() 轴上方使
轴上方使![]() 成立的点
成立的点![]() 只有一个.
只有一个.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 的两直线
的两直线![]() ,
,![]() 分别与椭圆
分别与椭圆![]() 交于点
交于点![]() ,
,![]() 和点
和点![]() ,
,![]() ,且
,且![]() ,比较
,比较![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com