
科目: 来源: 题型:
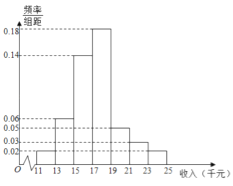
【题目】十九大以来,某贫困地区扶贫办积极贯彻落实国家精准扶贫的政策要求,带领广大农村地区人民群众脱贫奔小康.经过不懈的奋力拼搏,新农村建设取得巨大进步,农民收入也逐年增加.为了更好的制定2019年关于加快提升农民年收入力争早日脱贫的工作计划,该地扶贫办统计了2018年50位农民的年收入并制成如下频率分布直方图:
附:参考数据与公式 ![]() ,若
,若 ![]() ,则①
,则① ![]() ;②
;② ![]() ;③
;③ ![]() .
.
(1)根据频率分布直方图估计50位农民的年平均收入![]() (单位:千元)(同一组数据用该组数据区间的中点值表示);
(单位:千元)(同一组数据用该组数据区间的中点值表示);
(2)由频率分布直方图可以认为该贫困地区农民年收入 X 服从正态分布 ![]() ,其中
,其中![]() 近似为年平均收入
近似为年平均收入![]() 近似为样本方差
近似为样本方差![]() ,经计算得:
,经计算得:![]() ,利用该正态分布,求:
,利用该正态分布,求:
(i)在2019年脱贫攻坚工作中,若使该地区约有占总农民人数的84.14%的农民的年收入高于扶贫办制定的最低年收入标准,则最低年收入大约为多少千元?
(ii)为了调研“精准扶贫,不落一人”的政策要求落实情况,扶贫办随机走访了1000位农民.若每个农民的年收入相互独立,问:这1000位农民中的年收入不少于12.14千元的人数最有可能是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点,![]() 轴的非负半轴为极轴且取相同的单位长度建立极坐标系.直线
轴的非负半轴为极轴且取相同的单位长度建立极坐标系.直线![]() 的参数方程为
的参数方程为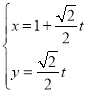 (
(![]() 为参数),圆
为参数),圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)写出直线![]() 的普通方程和圆
的普通方程和圆![]() 的极坐标方程;
的极坐标方程;
(2)已知点![]() ,直线
,直线![]() 与圆
与圆![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】近期,湖北省武汉市等多个地区发生新型冠状病毒感染的肺炎疫情.为了尽快遏制住疫情,我国科研工作者坚守在科研一线,加班加点争分夺秒与病毒抗争,夜以继日地进行研究.新型冠状病毒的潜伏期检测是疫情控制的关键环节之一.在传染病学中,通常把从致病刺激物侵入机体或对机体发生作用起,到机体出现反应或开始呈现该疾病对应的相关症状时止的这一阶段称为潜伏期.钟南山院士带领的研究团队统计了武汉市某地区10000名医学观察者的相关信息,并通过咽拭子核酸检测得到1000名确诊患者的信息如下表格:
潜伏期(单位:天) |
|
|
|
|
人数 | 800 | 190 | 8 | 2 |
(1)求这1000名确诊患者的潜伏期样本数据的平均数![]() (同一组数据用该组数据区间的中点值代表).
(同一组数据用该组数据区间的中点值代表).
(2)新型冠状病毒的潜伏期受诸多因素影响,为了研究潜伏期与患者性别的关系,以潜伏期是否超过7天为标准进行分层抽样,从上述1000名患者中抽取100名,得到如下列联表.请将列联表补充完整,并根据列联表判断是否有90%的把握认为潜伏期与患者性别有关.
潜伏期≤7天 | 潜伏期>7天 | 总计 | |
男性患者 | 12 | ||
女性患者 | 50 | ||
总计 | 100 |
(3)由于采样不当标本保存不当采用不同类型的标本以及使用不同厂家试剂都可能造成核酸检测结果“假阴性”而出现漏诊.当核酸检测呈阴性时,需要进一步进行血清学![]() 抗体检测,以弥补核酸检测漏诊的缺点.现对10名核酸检测结果呈阴性的人员逐一地进行血清检测,记每个人检测出
抗体检测,以弥补核酸检测漏诊的缺点.现对10名核酸检测结果呈阴性的人员逐一地进行血清检测,记每个人检测出![]() (
(![]() 是近期感染的标志)呈阳性的概率为
是近期感染的标志)呈阳性的概率为![]() 且相互独立,设至少检测了9个人才检测出
且相互独立,设至少检测了9个人才检测出![]() 呈阳性的概率为
呈阳性的概率为![]() ,求
,求![]() 取得最大值时相应的概率
取得最大值时相应的概率![]() .
.
附: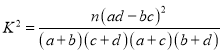 ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】半正多面体亦称“阿基米德多面体”,是由边数不全相同的正多边形为面的多面体,体现了数学的对称美.如图,将正方体沿交于一顶点的三条棱的中点截去一个三棱锥,如此共可截去八个三棱锥,得到一个有十四个面的半正多面体,它们的棱长都相等,其中八个为正三角形,六个为正方形,称这样的半正多面体为二十四等边体.若二十四等边体的棱长为2,则其体积为______;若其各个顶点都在同一个球面上,则该球的表面积为______.
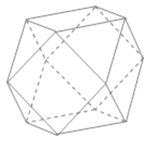
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以原点O为极点,
),以原点O为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)已知![]() ,曲线
,曲线![]() 与
与![]() 的交点A, B满足
的交点A, B满足![]() (A为第一象限的点),求
(A为第一象限的点),求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知经过圆![]() 上点
上点![]() 的切线方程是
的切线方程是![]() .
.
(1)类比上述性质,直接写出经过椭圆![]() 上一点
上一点![]() 的切线方程;
的切线方程;
(2)已知椭圆![]() ,P为直线
,P为直线![]() 上的动点,过P作椭圆E的两条切线,切点分别为AB,
上的动点,过P作椭圆E的两条切线,切点分别为AB,
①求证:直线AB过定点.
②当点P到直线AB的距离为![]() 时,求三角形PAB的外接圆方程.
时,求三角形PAB的外接圆方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年6月25日,《固体废物污染环境防治法(修订草案)》初次提请全国人大常委会审议,草案对“生活垃圾污染环境的防治”进行了专项规定.某小区采取一系列措施,宣传垃圾分类的知识与意义,并采购分类垃圾箱.为了了解垃圾分类的效果,该小区物业随机抽取了200位居民进行问卷调查,每位居民对小区采取的措施给出“满意”或“不满意”的评价.根据调查结果统计并做出年龄分布条形图和持不满意态度的居民的结构比例图,如图,在这200份问卷中,持满意态度的频率是0.65.
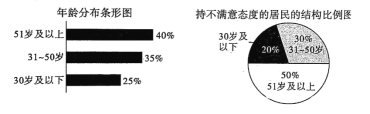
(1)完成下面的![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为“51岁及以上”和“50岁及以下”的居民对该小区采取的措施的评价有差异
的把握认为“51岁及以上”和“50岁及以下”的居民对该小区采取的措施的评价有差异
满意 | 不满意 | 总计 | |
51岁及以上的居民 | |||
50岁及以下的居民 | |||
总计 | 200 |
(2)按“51岁及以上”和“50岁及以下”的年龄段采取分层抽样的方法从中随机抽取5份,再从这5份调查问卷中随机抽取2份进行电话家访,求电话家访的两位居民恰好一位年龄在51岁及以上,另一位年龄在50岁及以下的概率.
| 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
附表及参考公式: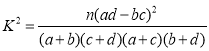 ,其中
,其中![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com