
科目: 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,左顶点为
,左顶点为![]() ,离心率为
,离心率为![]() ,点
,点![]() 是椭圆上的动点,
是椭圆上的动点,![]() 的面积的最大值为
的面积的最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设经过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() ,线段
,线段![]() 的中垂线为
的中垂线为![]() .若直线
.若直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,与直线
,与直线![]() 相交于点
相交于点![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某大型商场的空调在1月到5月的销售量与月份相关,得到的统计数据如下表:
月份 | 1 | 2 | 3 | 4 | 5 |
销量 | 0.6 | 0.8 | 1.2 | 1.6 | 1.8 |
(1)经分析发现1月到5月的销售量可用线性回归模型拟合该商场空调的月销量![]() (百件)与月份
(百件)与月份![]() 之间的相关关系.请用最小二乘法求
之间的相关关系.请用最小二乘法求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测6月份该商场空调的销售量;
,并预测6月份该商场空调的销售量;
(2)若该商场的营销部对空调进行新一轮促销,对7月到12月有购买空调意愿的顾客进行问卷调查.假设该地拟购买空调的消费群体十分庞大,经过营销部调研机构对其中的500名顾客进行了一个抽样调查,得到如下一份频数表:
有购买意愿对应的月份 | 7 | 8 | 9 | 10 | 11 | 12 |
频数 | 60 | 80 | 120 | 130 | 80 | 30 |
现采用分层抽样的方法从购买意愿的月份在7月与12月的这90名顾客中随机抽取6名,再从这6人中随机抽取3人进行跟踪调查,求抽出的3人中恰好有2人是购买意愿的月份是12月的概率.
参考公式与数据:线性回归方程![]() ,其中
,其中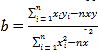 ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】为考察某动物疫苗预防某种疾病的效果,现对200只动物进行调研,并得到如下数据:
未发病 | 发病 | 合计 | |
未注射疫苗 | 20 | 60 | 80 |
注射疫苗 | 80 | 40 | 120 |
合计 | 100 | 100 | 200 |
(附: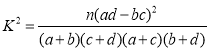 )
)
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
则下列说法正确的:( )
A.至少有99.9%的把握认为“发病与没接种疫苗有关”
B.至多有99%的把握认为“发病与没接种疫苗有关”
C.至多有99.9%的把握认为“发病与没接种疫苗有关”
D.“发病与没接种疫苗有关”的错误率至少有0.01%
查看答案和解析>>
科目: 来源: 题型:
【题目】“海水稻”就是耐盐碱水稻,是一种介于野生稻和栽培稻之间的普遍生长在海边滩涂地区,具有耐盐碱的水稻,它比其它普通的水稻均有更强的生存竞争能力,具有抗涝,抗病虫害,抗倒伏等特点,还具有预防和治疗多种疾病的功效,防癌效果尤为显著.海水稻的灌溉是将海水稀释后进行灌溉.某试验基地为了研究海水浓度![]() (‰)对亩产量
(‰)对亩产量![]() (吨)的影响,通过在试验田的种植实验,测得了某种海水稻的亩产量与海水浓度的数据如表.绘制散点图发现,可用线性回归模型拟合亩产量
(吨)的影响,通过在试验田的种植实验,测得了某种海水稻的亩产量与海水浓度的数据如表.绘制散点图发现,可用线性回归模型拟合亩产量![]() 与海水浓度
与海水浓度![]() 之间的相关关系,用最小二乘法计算得
之间的相关关系,用最小二乘法计算得![]() 与
与![]() 之间的线性回归方程为
之间的线性回归方程为![]() .
.
海水浓度 | 3 | 4 | 5 | 6 | 7 |
亩产量 | 0.62 | 0.58 | 0.49 | 0.4 | 0.31 |
残差 |
(1)请你估计:当浇灌海水浓度为8‰时,该品种的亩产量.
(2)①完成上述残差表:
②统计学中,常用相关指数![]() 来刻画回归效果,
来刻画回归效果,![]() 越大,模型拟合效果越好,并用它来说明预报变量与解释变量的相关性.你能否利用以上表格中的数据,利用统计学的相关知识,说明浇灌海水浓度对亩产量的贡献率?(计算中数据精确到
越大,模型拟合效果越好,并用它来说明预报变量与解释变量的相关性.你能否利用以上表格中的数据,利用统计学的相关知识,说明浇灌海水浓度对亩产量的贡献率?(计算中数据精确到![]() )
)
(附:残差公式![]() ,相关指数
,相关指数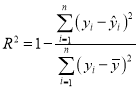 )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点![]() ,过点
,过点![]() 作抛物线
作抛物线![]() 的两切线,切点为
的两切线,切点为![]() .
.
(1)求两切点![]() 所在的直线方程;
所在的直线方程;
(2)椭圆![]() ,离心率为
,离心率为![]() ,(1)中直线AB与椭圆交于点P,Q,直线
,(1)中直线AB与椭圆交于点P,Q,直线![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,
,![]() ,若
,若![]() ,求椭圆的方程.
,求椭圆的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知定义域为R的奇函数![]() ,满足
,满足 ,则下列叙述正确的为( )
,则下列叙述正确的为( )
①存在实数k,使关于x的方程![]() 有7个不相等的实数根
有7个不相等的实数根
②当![]() 时,恒有
时,恒有![]()
③若当![]() 时,
时,![]() 的最小值为1,则
的最小值为1,则![]()
④若关于![]() 的方程
的方程![]() 和
和![]() 的所有实数根之和为零,则
的所有实数根之和为零,则![]()
A.①②③B.①③C.②④D.①②③④
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆C:![]() (a>b>0)的左右焦点分别为F1,F2点.M为椭圆上的一动点,△MF1F2面积的最大值为4.过点F2的直线l被椭圆截得的线段为PQ,当l⊥x轴时,
(a>b>0)的左右焦点分别为F1,F2点.M为椭圆上的一动点,△MF1F2面积的最大值为4.过点F2的直线l被椭圆截得的线段为PQ,当l⊥x轴时,![]() .
.
(1)求椭圆C的方程;
(2)过点F1作与x轴不重合的直线l,l与椭圆交于A,B两点,点A在直线![]() 上的投影N与点B的连线交x轴于D点,D点的横坐标x0是否为定值?若是,求出定值;若不是,请说明理由.
上的投影N与点B的连线交x轴于D点,D点的横坐标x0是否为定值?若是,求出定值;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com