
科目: 来源: 题型:
【题目】党的十九大明确把精准脱贫作为决胜全面建成小康社会必须打好的三大攻坚战之一,为坚决打赢脱贫攻坚战,某帮扶单位考察了甲乙两种不同的农产品加工生产方式,现对两种生产方式加工的产品质量进行测试并打分对比,得到如下数据:
生产方式甲 | 分值区间 |
|
|
|
|
|
频数 | 20 | 30 | 100 | 40 | 10 | |
生产方式乙 | 分值区间 |
|
|
|
|
|
频数 | 25 | 35 | 50 | 30 |
其中产品质量按测试指标可划分为:指标在区间![]() 上的为特优品,指标在区间
上的为特优品,指标在区间![]() 上的为一等品,指标在区间
上的为一等品,指标在区间![]() 上的为二等品.
上的为二等品.
(1)用事件![]() 表示“按照生产方式甲生产的产品为特优品”,估计
表示“按照生产方式甲生产的产品为特优品”,估计![]() 的概率;
的概率;
(2)填写下面列联表,并根据列联表判断能否有![]() 的把握认为“特优品”与生产方式有关?
的把握认为“特优品”与生产方式有关?
特优品 | 非特优品 | |
生产方式甲 | ||
生产方式乙 |
(3)根据打分结果对甲乙两种生产方式进行优劣比较.
附表:
| 0.10 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
参考公式: ,其中
,其中![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】一对夫妇为了给他们的独生孩子支付将来上大学的费用,从孩子一周岁生日开始,每年到银行储蓄![]() 元一年定期,若年利率为
元一年定期,若年利率为![]() 保持不变,且每年到期时存款(含利息)自动转为新的一年定期,当孩子18岁生日时不再存入,将所有存款(含利息)全部取回,则取回的钱的总数为
保持不变,且每年到期时存款(含利息)自动转为新的一年定期,当孩子18岁生日时不再存入,将所有存款(含利息)全部取回,则取回的钱的总数为![]()
![]()
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】以直角坐标系![]() 的原点为极点,x轴的非负半轴为极轴建立极坐标系,并且在两种坐标系中取相同的长度单位.若将曲线
的原点为极点,x轴的非负半轴为极轴建立极坐标系,并且在两种坐标系中取相同的长度单位.若将曲线![]() (
(![]() 为参数)上每一点的横坐标变为原来的
为参数)上每一点的横坐标变为原来的![]() (纵坐标不变),然后将所得图象向右平移2个单位,再向上平移3个单位得到曲线C.直线l的极坐标方程为
(纵坐标不变),然后将所得图象向右平移2个单位,再向上平移3个单位得到曲线C.直线l的极坐标方程为![]() .
.
(1)求曲线C的普通方程;
(2)设直线l与曲线C交于A,B两点,与x轴交于点P,线段AB的中点为M,求![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的中心在原点,左焦点
的中心在原点,左焦点![]() 、右焦点
、右焦点![]() 都在
都在![]() 轴上,点
轴上,点![]() 是椭圆
是椭圆![]() 上的动点,
上的动点,![]() 的面积的最大值为
的面积的最大值为![]() ,在
,在![]() 轴上方使
轴上方使![]() 成立的点
成立的点![]() 只有一个.
只有一个.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 的两直线
的两直线![]() ,
,![]() 分别与椭圆
分别与椭圆![]() 交于点
交于点![]() ,
,![]() 和点
和点![]() ,
,![]() ,且
,且![]() ,比较
,比较![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
科目: 来源: 题型:
【题目】在贯彻中共中央国务院关于精准扶贫政策的过程中,某单位定点帮扶甲、乙两个村各50户贫困户.为了做到精准帮扶,工作组对这100户村民的年收入情况、劳动能力情况、子女受教育情况、危旧房情况、患病情况等进行调查,并把调查结果转化为各户的贫困指标![]() 和
和![]() ,制成下图,其中“
,制成下图,其中“![]() ”表示甲村贫困户,“
”表示甲村贫困户,“![]() ”表示乙村贫困户.
”表示乙村贫困户.
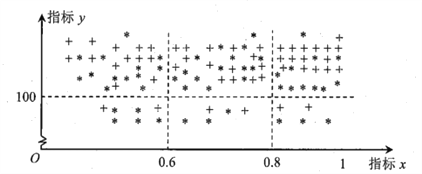
若![]() ,则认定该户为“绝对贫困户”,若
,则认定该户为“绝对贫困户”,若![]() ,则认定该户为“相对贫困户”,若
,则认定该户为“相对贫困户”,若![]() ,则认定该户为“低收入户”;
,则认定该户为“低收入户”;
若![]() ,则认定该户为“今年能脱贫户”,否则为“今年不能脱贫户”.
,则认定该户为“今年能脱贫户”,否则为“今年不能脱贫户”.
(1)从甲村50户中随机选出一户,求该户为“今年不能脱贫的绝对贫困户”的概率;
(2)若从所有“今年不能脱贫的非绝对贫困户”中选3户,用![]() 表示所选3户中乙村的户数,求
表示所选3户中乙村的户数,求![]() 的分布列和数学期望
的分布列和数学期望![]() ;
;
(3)试比较这100户中,甲、乙两村指标![]() 的方差的大小(只需写出结论).
的方差的大小(只需写出结论).
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() 的焦点为F,过点F,斜率为1的直线与抛物线C交于点A,B,且
的焦点为F,过点F,斜率为1的直线与抛物线C交于点A,B,且![]() .
.
(1)求抛物线C的方程;
(2)过点Q(1,1)作直线交抛物线C于不同于R(1,2)的两点D、E,若直线DR,ER分别交直线![]() 于M,N两点,求|MN|取最小值时直线DE的方程.
于M,N两点,求|MN|取最小值时直线DE的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com