
科目: 来源: 题型:
【题目】已知![]() ,
,![]() ,其中常数
,其中常数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的极值;
的极值;
(2)若函数![]() 有两个零点
有两个零点![]() ,求实数
,求实数![]() 的范围;
的范围;
(3)设![]() ,在区间
,在区间![]() 内是否存在区间
内是否存在区间![]() ,使函数
,使函数![]() 在区间
在区间![]() 的值域也是
的值域也是![]() ?请给出结论,并说明理由.
?请给出结论,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知等差数列![]() 和等比数列
和等比数列![]() 的各项均为整数,它们的前
的各项均为整数,它们的前![]() 项和分别为
项和分别为![]() ,且
,且![]() ,
,![]() .
.
(1)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(2)求![]() ;
;
(3)是否存在正整数![]() ,使得
,使得![]() 恰好是数列
恰好是数列![]() 或
或![]() 中的项?若存在,求出所有满足条件的
中的项?若存在,求出所有满足条件的![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某房地产商建有三栋楼宇![]() ,三楼宇间的距离都为2千米,拟准备在此三楼宇围成的区域
,三楼宇间的距离都为2千米,拟准备在此三楼宇围成的区域![]() 外建第四栋楼宇
外建第四栋楼宇![]() ,规划要求楼宇
,规划要求楼宇![]() 对楼宇
对楼宇![]() ,
,![]() 的视角为
的视角为![]() ,如图所示,假设楼宇大小高度忽略不计.
,如图所示,假设楼宇大小高度忽略不计.
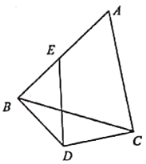
(1)求四栋楼宇围成的四边形区域![]() 面积的最大值;
面积的最大值;
(2)当楼宇![]() 与楼宇
与楼宇![]() ,
,![]() 间距离相等时,拟在楼宇
间距离相等时,拟在楼宇![]() ,
,![]() 间建休息亭
间建休息亭![]() ,在休息亭
,在休息亭![]() 和楼宇
和楼宇![]() ,
,![]() 间分别铺设鹅卵石路
间分别铺设鹅卵石路![]() 和防腐木路
和防腐木路![]() ,如图,已知铺设鹅卵石路、防腐木路的单价分别为
,如图,已知铺设鹅卵石路、防腐木路的单价分别为![]() ,
,![]() (单位:元千米,
(单位:元千米,![]() 为常数).记
为常数).记![]() ,求铺设此鹅卵石路和防腐木路的总费用的最小值.
,求铺设此鹅卵石路和防腐木路的总费用的最小值.
查看答案和解析>>
科目: 来源: 题型:
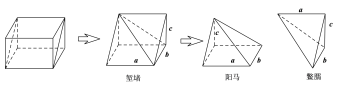
【题目】我国古代劳动人民在筑城、筑堤、挖沟、挖渠、建仓、建囤等工程中,积累了丰富的经验,总结出了一套有关体积、容积计算的方法,这些方法以实际问题的形式被收入我国古代数学名著《九章算术》中.《九章算术![]() 商功》:“斜解立方,得两堑堵.斜解堑堵,其一为阳马,一为鳖臑.阳马居二,鳖臑居一,不易之率也.合两鳖臑三而一,验之以棊,其形露矣.”下图解释了这段话中由一个长方体,得到“堑堵”、“阳马”、“鳖臑”的过程.已知如图堑堵的棱长
商功》:“斜解立方,得两堑堵.斜解堑堵,其一为阳马,一为鳖臑.阳马居二,鳖臑居一,不易之率也.合两鳖臑三而一,验之以棊,其形露矣.”下图解释了这段话中由一个长方体,得到“堑堵”、“阳马”、“鳖臑”的过程.已知如图堑堵的棱长![]() ,则鳖臑的外接球的体积为_________.
,则鳖臑的外接球的体积为_________.
查看答案和解析>>
科目: 来源: 题型:
【题目】在测试中,客观题难题的计算公式为![]() ,其中
,其中![]() 为第
为第![]() 题的难度,
题的难度, ![]() 为答对该题的人数,
为答对该题的人数, ![]() 为参加测试的总人数.现对某校高三年级120名学生进行一次测试,共5道客观题.测试前根据对学生的了解,预估了每道题的难度,如下表所示:
为参加测试的总人数.现对某校高三年级120名学生进行一次测试,共5道客观题.测试前根据对学生的了解,预估了每道题的难度,如下表所示:

测试后,从中随机抽取了10名学生,将他们编号后统计各题的作答情况,如下表所示(“√”表示答对,“×”表示答错):
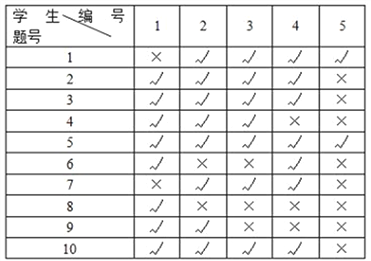
(1)根据题中数据,将抽样的10名学生每道题实测的答对人数及相应的实测难度填入下表,并估计这120名学生中第5题的实测答对人数;

(2)从编号为1到5的5人中随机抽取2人,求恰好有1人答对第5题的概率;
(3)定义统计量![]() ,其中
,其中![]() 为第
为第![]() 题的实测难度,
题的实测难度, ![]() 为第
为第![]() 题的预估难度(
题的预估难度(![]() ).规定:若
).规定:若![]() ,则称该次测试的难度预估合理,否则为不合理.判断本次测试的难度预估是否合理.
,则称该次测试的难度预估合理,否则为不合理.判断本次测试的难度预估是否合理.
查看答案和解析>>
科目: 来源: 题型:
【题目】健身馆某项目收费标准为每次60元,现推出会员优惠活动:具体收费标准如下:
消费次数 | 第1次 | 第2次 | 第3次 | 不少于4次 |
收费比例 | 0.95 | 0.90 | 0.85 | 0.80 |
现随机抽取了100位会员统计它们的消费次数,得到数据如下:
消费次数 | 1次 | 2次 | 3次 | 不少于4次 |
频数 | 60 | 25 | 10 | 5 |
假设该项目的成本为每次30元,根据给出的数据回答下列问题:
(1)估计1位会员至少消费两次的概率
(2)某会员消费4次,求这4次消费获得的平均利润;
查看答案和解析>>
科目: 来源: 题型:
【题目】从一批苹果中,随机抽取50个,其重量(单位:克)的频数分布表如下:
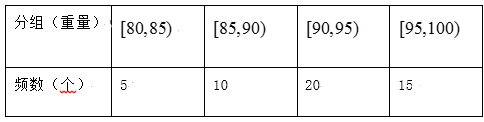
(1)根据频数分布表计算苹果的重量在![]() 的频率;
的频率;
(2)用分层抽样的方法从重量在![]() 和
和![]() 的苹果中共抽取4个,其中重量在
的苹果中共抽取4个,其中重量在![]() 的有几个?
的有几个?
(3)在(2)中抽出的4个苹果中,任取2个,写出所有可能的结果,并求重量在![]() 和
和![]() 中各有1个的概率.
中各有1个的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】小赵和小王约定在早上![]() 至
至![]() 之间到某公交站搭乘公交车去上学,已知在这段时间内,共有
之间到某公交站搭乘公交车去上学,已知在这段时间内,共有![]() 班公交车到达该站,到站的时间分别为
班公交车到达该站,到站的时间分别为![]() ,
,![]() ,如果他们约定见车就搭乘,则小赵和小王恰好能搭乘同一班公交车去上学的概率为__________.
,如果他们约定见车就搭乘,则小赵和小王恰好能搭乘同一班公交车去上学的概率为__________.
查看答案和解析>>
科目: 来源: 题型:
【题目】小明家的晚报在下午![]() 任何一个时间随机地被送到,他们一家人在下午
任何一个时间随机地被送到,他们一家人在下午![]() 任何一个时间随机地开始晚餐.为了计算晚报在晚餐开始之前被送到的概率,某小组借助随机数表的模拟方法来计算概率,他们的具体做法是将每个1分钟的时间段看作个体进行编号,
任何一个时间随机地开始晚餐.为了计算晚报在晚餐开始之前被送到的概率,某小组借助随机数表的模拟方法来计算概率,他们的具体做法是将每个1分钟的时间段看作个体进行编号,![]() 编号为01,
编号为01,![]() 编号为02,依此类推,
编号为02,依此类推,![]() 编号为90.在随机数表中每次选取一个四位数,前两位表示晚报时间,后两位表示晚餐时间,如果读取的四位数表示的晚报晚餐时间有一个不符合实际意义,视为这次读取的无效数据(例如下表中的第一个四位数7840中的78不符合晚报时间).按照从左向右,读完第一行,再从左向右读第二行的顺序,读完下表,用频率估计晚报在晚餐开始之前被送到的概率为
编号为90.在随机数表中每次选取一个四位数,前两位表示晚报时间,后两位表示晚餐时间,如果读取的四位数表示的晚报晚餐时间有一个不符合实际意义,视为这次读取的无效数据(例如下表中的第一个四位数7840中的78不符合晚报时间).按照从左向右,读完第一行,再从左向右读第二行的顺序,读完下表,用频率估计晚报在晚餐开始之前被送到的概率为![]()
![]()
7840 1160 5054 3139 8082 7732 5034 3682 4829 4052 |
4201 6277 5678 5188 6854 0200 8650 7584 0136 7655 |
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com