A.85%B.75%C.63.5%D.67.5%

【题目】已知，函数，其中e=2.71828…为自然对数的底数．

（Ⅰ）证明：函数在上有唯一零点；

（Ⅱ）记x0为函数在上的零点，证明：

（ⅰ）；

（ⅱ）．

【题目】如图，已知椭圆，抛物线，点A是椭圆与抛物线的交点，过点A的直线l交椭圆于点B，交抛物线于M（B，M不同于A）．

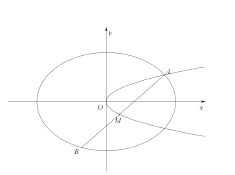
（Ⅰ）若，求抛物线的焦点坐标；

（Ⅱ）若存在不过原点的直线l使M为线段AB的中点，求p的最大值．

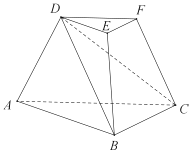
（I）证明：EF⊥DB；

（II）求DF与面DBC所成角的正弦值．

【题目】设集合S，T，SN*，TN*，S，T中至少有两个元素，且S，T满足：

①对于任意x，yS，若x≠y，都有xyT

②对于任意x，yT，若x<y，则S；

下列命题正确的是（ ）

A.若S有4个元素，则S∪T有7个元素

B.若S有4个元素，则S∪T有6个元素

C.若S有3个元素，则S∪T有5个元素

D.若S有3个元素，则S∪T有4个元素

【题目】高铁是我国国家名片之一，高铁的修建凝聚着中国人的智慧与汗水.如图所示，B、E、F为山脚两侧共线的三点，在山顶A处测得这三点的俯角分别为、、，计划沿直线BF开通穿山隧道，现已测得BC、DE、EF三段线段的长度分别为3、1、2.

（1）求出线段AE的长度；

（2）求出隧道CD的长度.

（1）若甲同学每次投篮命中的概率为，且相互不影响，记甲同学投完三次后的总分为X，求随机变量X的概率分布列；

（2）若（1）中的甲同学邀请乙同学一起参加投篮项目，已知乙同学每次投篮命中的概率为，且相互不影响，甲、乙两人之间互不干扰.求甲同学的总分低于乙同学的总分的概率.

【题目】已知是各项均为正数的无穷数列，且满足，.

（1）若，，求a的值；

（2）设数列满足，其前n项的和为.

①求证：是等差数列；

②若对于任意的，都存在，使得成立.求证：.

【题目】设，，，其中e为自然对数的底数（）.

（1）当时，求在处的切线方程；

（2）设，求的单调区间；

（3）当时，恒成立，求a的取值范围.

【题目】如图，在平面直角坐标系中，已知椭圆，其右焦点F到其右准线的距离为1，离心率为，A，B分别为椭圆的上、下顶点，过点F且不与x轴重合的直线l与椭圆交于C，D两点，与y轴交于点P，直线与交于点Q.

（1）求椭圆的标准方程；

（2）当时，求直线的方程；

（3）求证：为定值.