
科目: 来源: 题型:
【题目】基本再生数R0与世代间隔T是新冠肺炎的流行病学基本参数.基本再生数指一个感染者传染的平均人数,世代间隔指相邻两代间传染所需的平均时间.在新冠肺炎疫情初始阶段,可以用指数模型:![]() 描述累计感染病例数I(t)随时间t(单位:天)的变化规律,指数增长率r与R0,T近似满足R0 =1+rT.有学者基于已有数据估计出R0=3.28,T=6.据此,在新冠肺炎疫情初始阶段,累计感染病例数增加1倍需要的时间约为(ln2≈0.69) ( )
描述累计感染病例数I(t)随时间t(单位:天)的变化规律,指数增长率r与R0,T近似满足R0 =1+rT.有学者基于已有数据估计出R0=3.28,T=6.据此,在新冠肺炎疫情初始阶段,累计感染病例数增加1倍需要的时间约为(ln2≈0.69) ( )
A.1.2天B.1.8天
C.2.5天D.3.5天
查看答案和解析>>
科目: 来源: 题型:
【题目】某中学的学生积极参加体育锻炼,其中有96%的学生喜欢足球或游泳,60%的学生喜欢足球,82%的学生喜欢游泳,则该中学既喜欢足球又喜欢游泳的学生数占该校学生总数的比例是( )
A.62%B.56%
C.46%D.42%
查看答案和解析>>
科目: 来源: 题型:
【题目】日晷是中国古代用来测定时间的仪器,利用与晷面垂直的晷针投射到晷面的影子来测定时间.把地球看成一个球(球心记为O),地球上一点A的纬度是指OA与地球赤道所在平面所成角,点A处的水平面是指过点A且与OA垂直的平面.在点A处放置一个日晷,若晷面与赤道所在平面平行,点A处的纬度为北纬40°,则晷针与点A处的水平面所成角为( )

A.20°B.40°
C.50°D.90°
查看答案和解析>>
科目: 来源: 题型:
【题目】信息熵是信息论中的一个重要概念.设随机变量X所有可能的取值为![]() ,且
,且![]() ,定义X的信息熵
,定义X的信息熵![]() .( )
.( )
A.若n=1,则H(X)=0
B.若n=2,则H(X)随着![]() 的增大而增大
的增大而增大
C.若![]() ,则H(X)随着n的增大而增大
,则H(X)随着n的增大而增大
D.若n=2m,随机变量Y所有可能的取值为![]() ,且
,且![]() ,则H(X)≤H(Y)
,则H(X)≤H(Y)
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系xOy中,曲线C的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() ,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系.
,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系.
(1)求直线l和曲线C的极坐标方程;
(2)若直线![]() 与直线l相交于点A,与曲线C相交于不同的两点M,N.求
与直线l相交于点A,与曲线C相交于不同的两点M,N.求![]() 的最小值.
的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知O为原点,抛物线![]() 的准线与y轴的交点为H,P为抛物线C上横坐标为4的点,已知点P到准线的距离为5.
的准线与y轴的交点为H,P为抛物线C上横坐标为4的点,已知点P到准线的距离为5.
(1)求C的方程;
(2)过C的焦点F作直线l与抛物线C交于A,B两点,若以AH为直径的圆过B,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】政府工作报告指出,2019年我国深入实施创新驱动发展战略,创新能力和效率进一步提升;2020年要提升科技支撑能力,健全以企业为主体的产学研一体化创新机制,某企业为了提升行业核心竞争力,逐渐加大了科技投入;该企业连续5年来的科技投入x(百万元)与收益y(百万元)的数据统计如下:
科技投入x | 1 | 2 | 3 | 4 | 5 |
收益y | 40 | 50 | 60 | 70 | 90 |
(1)请根据表中数据,建立y关于x的线性回归方程;
(2)按照(1)中模型,已知科技投入8百万元时收益为140百万元,求残差![]() (残差
(残差![]() 真实值-预报值).
真实值-预报值).
参考数据:回归直线方程![]() ,其中
,其中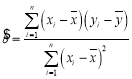 .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱柱![]() 中,四边形ABCD是边长等于2的菱形,
中,四边形ABCD是边长等于2的菱形,![]() ,
,![]() 平面ABCD,O,E分别是
平面ABCD,O,E分别是![]() ,AB的中点,AC交DE于点H,点F为HC的中点
,AB的中点,AC交DE于点H,点F为HC的中点
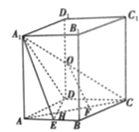
(1)求证:![]() 平面
平面![]() ;
;
(2)若OF与平面ABCD所成的角为60°,求三棱锥![]() 的表面积.
的表面积.
查看答案和解析>>
科目: 来源: 题型:
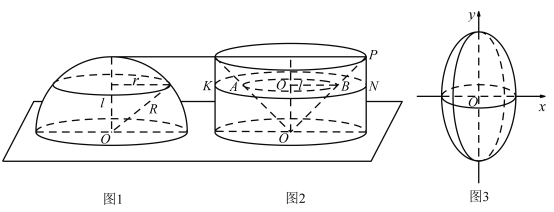
【题目】运用祖暅原理计算球的体积时,夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意一个平面所截,若截面面积都相等,则这两个几何体的体积相等.构造一个底面半径和高都与球的半径相等的圆柱,与半球(如图①)放置在同一平面上,然后在圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥后得到一新几何体(如图②),用任何一个平行于底面的平面去截它们时,可证得所截得的两个截面面积相等,由此可证明新几何体与半球体积相等.现将椭圆![]() 绕y轴旋转一周后得一橄榄状的几何体(如图③),类比上述方法,运用祖暅原理可求得其体积等于( )
绕y轴旋转一周后得一橄榄状的几何体(如图③),类比上述方法,运用祖暅原理可求得其体积等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com