
科目: 来源: 题型:
【题目】在①![]() ;②
;②![]() ;③
;③![]()
![]() ,这三个条件中任选一个,补充在下面问题中,然后解答补充完整的题目.
,这三个条件中任选一个,补充在下面问题中,然后解答补充完整的题目.
在△![]() 中,内角A,B,C所对的边分别为
中,内角A,B,C所对的边分别为![]() .且满足_________.
.且满足_________.
(1)求![]() ;
;
(2)已知![]() ,△
,△![]() 的外接圆半径为
的外接圆半径为![]() ,求△
,求△![]() 的边AB上的高
的边AB上的高![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】CES是世界上最大的消费电子技术展,也是全球最大的消费技术产业盛会.2020CES消费电子展于2020年1月7日—10日在美国拉斯维加斯举办.在这次CES消费电子展上,我国某企业发布了全球首款彩色水墨屏阅读手机,惊艳了全场.若该公司从7名员工中选出3名员工负责接待工作(这3名员工的工作视为相同的工作),再选出2名员工分别在上午、下午讲解该款手机性能,若其中甲和乙至多有1人负责接待工作,则不同的安排方案共有__________种.
查看答案和解析>>
科目: 来源: 题型:
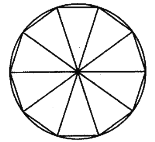
【题目】在3世纪中期,我国古代数学家刘徽在《九章算术注》中提出了割圆术:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣”.这可视为中国古代极限观念的佳作.割圆术可以视为将一个圆内接正![]() 边形等分成
边形等分成![]() 个等腰三角形(如图所示),当
个等腰三角形(如图所示),当![]() 变得很大时,等腰三角形的面积之和近似等于圆的面积.运用割圆术的思想,可得到sin3°的近似值为( )(
变得很大时,等腰三角形的面积之和近似等于圆的面积.运用割圆术的思想,可得到sin3°的近似值为( )(![]() 取近似值3.14)
取近似值3.14)
A.0.012B.0.052
C.0.125D.0.235
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,点
上,点![]() 在圆
在圆![]() 上,且圆
上,且圆![]() 上的所有点均在椭圆
上的所有点均在椭圆![]() 外,若
外,若![]() 的最小值为
的最小值为![]() ,且椭圆
,且椭圆![]() 的长轴长恰与圆
的长轴长恰与圆![]() 的直径长相等,则下列说法正确的是( )
的直径长相等,则下列说法正确的是( )
A.椭圆![]() 的焦距为
的焦距为![]() B.椭圆
B.椭圆![]() 的短轴长为
的短轴长为![]()
C.![]() 的最小值为
的最小值为![]() D.过点
D.过点![]() 的圆
的圆![]() 的切线斜率为
的切线斜率为![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,且过点A(2,1).
,且过点A(2,1).
(1)求C的方程:
(2)点M,N在C上,且AM⊥AN,AD⊥MN,D为垂足.证明:存在定点Q,使得|DQ|为定值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四棱锥P-ABCD的底面为正方形,PD⊥底面ABCD.设平面PAD与平面PBC的交线为l.
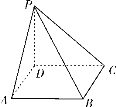
(1)证明:l⊥平面PDC;
(2)已知PD=AD=1,Q为l上的点,求PB与平面QCD所成角的正弦值的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】为加强环境保护,治理空气污染,环境监测部门对某市空气质量进行调研,随机抽查了![]() 天空气中的
天空气中的![]() 和
和![]() 浓度(单位:
浓度(单位:![]() ),得下表:
),得下表:
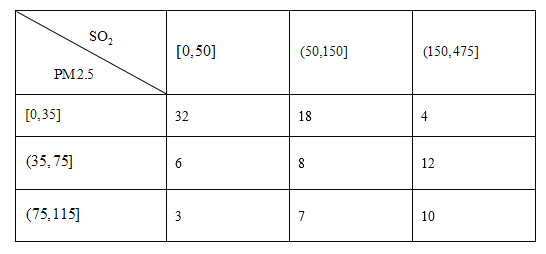
(1)估计事件“该市一天空气中![]() 浓度不超过
浓度不超过![]() ,且
,且![]() 浓度不超过
浓度不超过![]() ”的概率;
”的概率;
(2)根据所给数据,完成下面的![]() 列联表:
列联表:
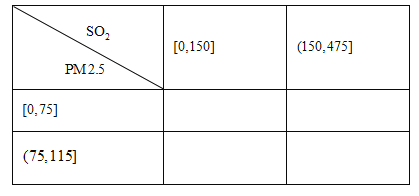
(3)根据(2)中的列联表,判断是否有![]() 的把握认为该市一天空气中
的把握认为该市一天空气中![]() 浓度与
浓度与![]() 浓度有关?
浓度有关?
附: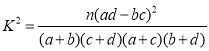 ,
,
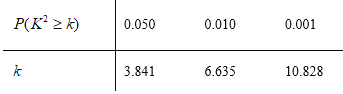
查看答案和解析>>
科目: 来源: 题型:
【题目】在①![]() ,②
,②![]() ,③
,③![]() 这三个条件中任选一个,补充在下面问题中,若问题中的三角形存在,求
这三个条件中任选一个,补充在下面问题中,若问题中的三角形存在,求![]() 的值;若问题中的三角形不存在,说明理由.
的值;若问题中的三角形不存在,说明理由.
问题:是否存在![]() ,它的内角
,它的内角![]() 的对边分别为
的对边分别为![]() ,且
,且![]() ,
,![]() ,________?
,________?
注:如果选择多个条件分别解答,按第一个解答计分.
查看答案和解析>>
科目: 来源: 题型:
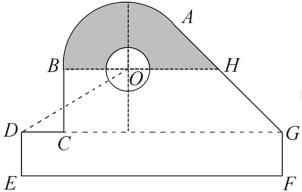
【题目】某中学开展劳动实习,学生加工制作零件,零件的截面如图所示.O为圆孔及轮廓圆弧AB所在圆的圆心,A是圆弧AB与直线AG的切点,B是圆弧AB与直线BC的切点,四边形DEFG为矩形,BC⊥DG,垂足为C,tan∠ODC=![]() ,
,![]() ,EF=12 cm,DE=2 cm,A到直线DE和EF的距离均为7 cm,圆孔半径为1 cm,则图中阴影部分的面积为________cm2.
,EF=12 cm,DE=2 cm,A到直线DE和EF的距离均为7 cm,圆孔半径为1 cm,则图中阴影部分的面积为________cm2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com