
科目: 来源: 题型:
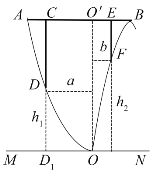
【题目】某地准备在山谷中建一座桥梁,桥址位置的竖直截面图如图所示:谷底O在水平线MN上,桥AB与MN平行,![]() 为铅垂线(
为铅垂线(![]() 在AB上).经测量,左侧曲线AO上任一点D到MN的距离
在AB上).经测量,左侧曲线AO上任一点D到MN的距离![]() (米)与D到
(米)与D到![]() 的距离a(米)之间满足关系式
的距离a(米)之间满足关系式![]() ;右侧曲线BO上任一点F到MN的距离
;右侧曲线BO上任一点F到MN的距离![]() (米)与F到
(米)与F到![]() 的距离b(米)之间满足关系式
的距离b(米)之间满足关系式![]() .已知点B到
.已知点B到![]() 的距离为40米.
的距离为40米.
(1)求桥AB的长度;
(2)计划在谷底两侧建造平行于![]() 的桥墩CD和EF,且CE为80米,其中C,E在AB上(不包括端点).桥墩EF每米造价k(万元)、桥墩CD每米造价
的桥墩CD和EF,且CE为80米,其中C,E在AB上(不包括端点).桥墩EF每米造价k(万元)、桥墩CD每米造价![]() (万元)(k>0).问
(万元)(k>0).问![]() 为多少米时,桥墩CD与EF的总造价最低?
为多少米时,桥墩CD与EF的总造价最低?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的一个顶点为
的一个顶点为![]() ,右焦点为
,右焦点为![]() ,且
,且![]() ,其中
,其中![]() 为原点.
为原点.
(Ⅰ)求椭圆的方程;
(Ⅱ)已知点![]() 满足
满足![]() ,点
,点![]() 在椭圆上(
在椭圆上(![]() 异于椭圆的顶点),直线
异于椭圆的顶点),直线![]() 与以
与以![]() 为圆心的圆相切于点
为圆心的圆相切于点![]() ,且
,且![]() 为线段
为线段![]() 的中点.求直线
的中点.求直线![]() 的方程.
的方程.
查看答案和解析>>
科目: 来源: 题型:
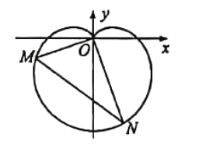
【题目】在新中国成立70周年国庆阅兵庆典中,众多群众在脸上贴着一颗红心,以此表达对祖国的热爱之情,在数学中,有多种方程都可以表示心型曲线,其中有著名的笛卡尔心型曲线,如图,在直角坐标系中,以原点O为极点,x轴正半轴为极轴建立极坐标系.图中的曲线就是笛卡尔心型曲线,其极坐标方程为![]() (
(![]() ),M为该曲线上的任意一点.
),M为该曲线上的任意一点.
(1)当![]() 时,求M点的极坐标;
时,求M点的极坐标;
(2)将射线OM绕原点O逆时针旋转![]() 与该曲线相交于点N,求
与该曲线相交于点N,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年春节期间,某超市准备举办一次有奖促销活动,若顾客一次消费达到400元则可参加一次抽奖活动,超市设计了两种抽奖方案.
方案一:一个不透明的盒子中装有30个质地均匀且大小相同的小球,其中10个红球,20个白球,搅拌均匀后,顾客从中随机抽取一个球,若抽到红球则顾客获得60元的返金券,若抽到白球则获得20元的返金券,且顾客有放回地抽取3次.
方案二:一个不透明的盒子中装有30个质地均匀且大小相同的小球,其中10个红球,20个白球,搅拌均匀后,顾客从中随机抽取一个球,若抽到红球则顾客获得80元的返金券,若抽到白球则未中奖,且顾客有放回地抽取3次.
(1)现有两位顾客均获得抽奖机会,且都按方案一抽奖,试求这两位顾客均获得180元返金券的概率;
(2)若某顾客获得抽奖机会.
①试分别计算他选择两种抽奖方案最终获得返金券的数学期望;
②为了吸引顾客消费,让顾客获得更多金额的返金券,该超市应选择哪一种抽奖方案进行促销活动?
查看答案和解析>>
科目: 来源: 题型:
【题目】2020年春节突如其来的新型冠状病毒肺炎在湖北爆发,一方有难八方支援,全国各地的白衣天使走上战场的第一线,某医院抽调甲、乙两名医生,抽调![]() 、
、![]() 、
、![]() 三名护士支援武汉第一医院与第二医院,参加武汉疫情狙击战其中选一名护士与一名医生去第一医院,其它都在第二医院工作,则医生甲和护士
三名护士支援武汉第一医院与第二医院,参加武汉疫情狙击战其中选一名护士与一名医生去第一医院,其它都在第二医院工作,则医生甲和护士![]() 被选在第一医院工作的概率为( )
被选在第一医院工作的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com