
科目: 来源: 题型:
【题目】2020年春节前后,一场突如其来的新冠肺炎疫情在全国蔓延.疫情就是命令,防控就是责任.在党中央的坚强领导和统一指挥下,全国人民众志成城、团结一心,掀起了一场坚决打赢疫情防控阻击战的人民战争.下侧的图表展示了2月14日至29日全国新冠肺炎疫情变化情况,根据该折线图,下列结论正确的是( )
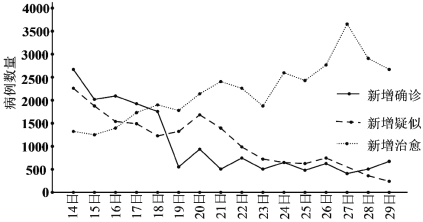
A.16天中每日新增确诊病例数量呈下降趋势且19日的降幅最大
B.16天中每日新增确诊病例的中位数大于新增疑似病例的中位数
C.16天中新增确诊、新增疑似、新增治愈病例的极差均大于![]()
D.19日至29日每日新增治愈病例数量均大于新增确诊与新增疑似病例之和
查看答案和解析>>
科目: 来源: 题型:
【题目】已知曲线C的极坐标方程是ρsin2θ-8cosθ=0.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系xOy.在直角坐标系中,倾斜角为α的直线l过点P(2,0).
(1)写出曲线C的直角坐标方程和直线l的参数方程;
(2)设点Q与点G的极坐标分别为![]() ,(2,π),若直线l经过点Q
,(2,π),若直线l经过点Q![]() ,且与曲线C相交于A,B两点,求△GAB的面积.
,且与曲线C相交于A,B两点,求△GAB的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】(本小题满分14分)已知过原点的动直线![]() 与圆
与圆![]()
![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() .
.
(1)求圆![]() 的圆心坐标;
的圆心坐标;
(2)求线段![]() 的中点
的中点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(3)是否存在实数![]() ,使得直线
,使得直线![]()
![]() 与曲线
与曲线![]() 只有一个交点?若存在,求出
只有一个交点?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年下半年以来,各地区陆续出台了“垃圾分类”的相关管理条例,实行“垃圾分类”能最大限度地减少垃圾处置量,实现垃圾资源利用,改善生存环境质量.某部门在某小区年龄处于区间![]() 内的人中随机抽取
内的人中随机抽取![]() 人进行了“垃圾分类”相关知识掌握和实施情况的调查,并把达到“垃圾分类”标准的人称为“环保族”,得到图各年龄段人数的频率分布直方图和表中统计数据.
人进行了“垃圾分类”相关知识掌握和实施情况的调查,并把达到“垃圾分类”标准的人称为“环保族”,得到图各年龄段人数的频率分布直方图和表中统计数据.
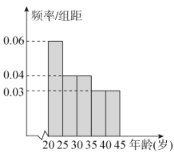
(1)求![]() 的值;
的值;
(2)根据频率分布直方图,估计这![]() 人年龄的平均值(同一组数据用该组区间的中点值代替,结果保留整数);
人年龄的平均值(同一组数据用该组区间的中点值代替,结果保留整数);
(3)从年龄段在![]() 的“环保族”中采用分层抽样的方法抽取9人进行专访,并在这9人中选取2人作为记录员,求选取的2名记录员中至少有一人年龄在区间
的“环保族”中采用分层抽样的方法抽取9人进行专访,并在这9人中选取2人作为记录员,求选取的2名记录员中至少有一人年龄在区间![]() 中的概率.
中的概率.
组数 | 分组 | “环保族”人数 | 占本组频率 |
第一组 |
| 45 | 0.75 |
第二组 |
| 25 |
|
第三组 |
|
| 0.5 |
第四组 |
| 3 | 0.2 |
第五组 |
| 3 | 0.1 |
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=(2﹣a)(x﹣1)﹣2lnx,g(x)= ![]() (a∈R,e为自然对数的底数)
(a∈R,e为自然对数的底数)
(Ⅰ)当a=1时,求f(x)的单调区间;
(Ⅱ)若函数f(x)在![]() 上无零点,求a的最小值;
上无零点,求a的最小值;
(Ⅲ)若对任意给定的x0∈(0,e],在(0,e]上总存在两个不同的xi(i=1,2),使得f(xi)=g(x0)成立,求a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() ,以椭圆的顶点为顶点的四边形的面积为
,以椭圆的顶点为顶点的四边形的面积为![]() ,且该四边形内切圆的半径为
,且该四边形内切圆的半径为![]() .
.
(1)求椭圆的方程;
(2)设![]() 是过椭圆中心的任意一条弦,直线
是过椭圆中心的任意一条弦,直线![]() 是线段
是线段![]() 的垂直平分线,若
的垂直平分线,若![]() 是直线
是直线![]() 与椭圆的一个交点,求
与椭圆的一个交点,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目: 来源: 题型:
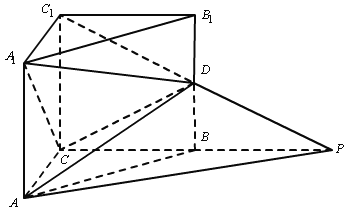
【题目】如图:在直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 是棱
是棱![]() 上一点,
上一点,![]() 是
是![]() 的延长线与
的延长线与![]() 的延长线的交点,且
的延长线的交点,且![]() 平面
平面![]() .
.
(1)求证:![]() ;
;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)若点![]() 在线段
在线段![]() 上,且直线
上,且直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com