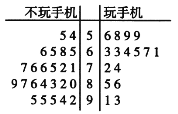
数学成绩不低于70分为良好，低于70分为一般．

（1）根据以上资料完成下面的列联表，并判断有多大把握认为“数学成绩良好与不玩手机有关系”．

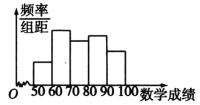
（2）现将40名同学的数学成绩分为如下5组：

，，，，．其频率分布直方图如图所示．计算这40名同学数学成绩的平均数，由茎叶图得到的真实值记为，由频率分布直方图得到的估计值记为（同一组中的数据用该组区间的中点值作代表），求与的误差值．

（3）从这40名同学数学成绩高于90分的7人中随机选取2人介绍学习方法，求这2保不玩手机的人数的分布列和数学期望．

附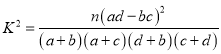：，这40名同学的数学成绩总和为2998分．

【题目】如图，平面，，点分别为的中点.

（Ⅰ）求证：平面；

（Ⅱ）求二面角的正弦值；

（Ⅲ）若为线段上的点，且直线与平面所成的角为，求线段的长.

【题目】已知平面内两个定点和点，是动点，且直线,的斜率乘积为常数，设点的轨迹为.

① 存在常数，使上所有点到两点距离之和为定值；

② 存在常数，使上所有点到两点距离之和为定值；

③ 不存在常数，使上所有点到两点距离差的绝对值为定值；

④ 不存在常数，使上所有点到两点距离差的绝对值为定值.

其中正确的命题是_______________.（填出所有正确命题的序号）

【题目】祖暅是我国南北朝时期杰出的数学家和天文学家祖冲之的儿子，他提出了一条原理：“幂势既同幂，则积不容异”.这里的“幂”指水平截面的面积，“势”指高.这句话的意思是：两个等高的几何体若在所有等高处的水平截面的面积相等，则这两个几何体体积相等.一般大型热电厂的冷却塔大都采用双曲线型.设某双曲线型冷却塔是曲线 与直线， 和所围成的平面图形绕轴旋转一周所得，如图所示.试应用祖暅原理类比求球体体积公式的方法，求出此冷却塔的体积为_______.

【题目】已知函数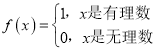，则下列判断中是真命题的有（ ）．

①，；②是偶函数；③对于任意一个非零有理数，，；④存在三个点，，，使得为等边三角形．

A.①②③B.①②③④C.①③④D.②③④

在直角坐标系xoy中，曲线的参数方程是（t是参数），以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线的极坐标方程是

(1)求曲线的普通方程和曲线的直角坐标方程；

(2)若两曲线交点为A、B，求

【题目】设函数.

（1）研究函数的极值点；

（2）当时，若对任意的，恒有，求的取值范围；

（3）证明：.

【题目】已知椭圆：的离心率为．

（1）求椭圆的方程．

（2）设直线过点且与椭圆交于，两点．过点作直线的垂线，垂足为．证明直线过定点．

某校研究学习小组从汽车市场上随机选取了辆纯电动乘用车，根据其续驶里程（单次充电后能行驶的最大里程）作出了如下的频率与频数的统计表：

（1）若从这辆纯电动乘用车中任选2辆，求选到的2辆车续驶里程都不低于150km的概率．

（2）若以频率作为概率，设为购买一辆纯电动乘用车获得的补贴，求的分布列和数学期望．

(1)证明:AE⊥PD;

(2)若AB=2,PA=2,求二面角E-AF-C的余弦值.