
科目: 来源: 题型:
【题目】党的十九大明确把精准脱贫作为决胜全面建成小康社会必须打好的三大攻坚战之一,为坚决打赢脱贫攻坚战,某帮扶单位为帮助定点扶贫村扶贫,此帮扶单位为了解该村贫困户对其所提供帮扶的满意度,随机调查了40个贫困户,得到贫困户的满意度评分如下:
贫困户 编号 | 评分 | 贫困户 编号 | 评分 | 贫困户 编号 | 评分 | 贫困户 编号 | 评分 | |||
1 | 78 | 11 | 88 | 21 | 79 | 31 | 93 | |||
2 | 73 | 12 | 86 | 22 | 83 | 32 | 78 | |||
3 | 81 | 13 | 95 | 23 | 72 | 33 | 75 | |||
4 | 92 | 14 | 76 | 24 | 74 | 34 | 81 | |||
5 | 86 | 15 | 80 | 25 | 93 | 35 | 89 | |||
6 | 85 | 16 | 78 | 26 | 66 | 36 | 77 | |||
7 | 79 | 17 | 88 | 27 | 80 | 37 | 81 | |||
8 | 84 | 18 | 82 | 28 | 83 | 38 | 76 | |||
9 | 63 | 19 | 76 | 29 | 74 | 39 | 85 | |||
10 | 85 | 20 | 87 | 30 | 82 | 40 | 78 |
用系统抽样法从40名贫困户中抽取容量为8的样本,且在第一分段里随机抽到的评分数据为86.
(1)请你列出抽到的8个样本的评分数据;
(2)计算所抽到的8个样本的均值![]() 和方差
和方差![]() ;
;
(3)在(2)条件下,若贫困户的满意度评分在![]() 之间,则满意度等级为“A级”.运用样本估计总体的思想,现从(1)中抽到的8个样本的满意度为“A级”贫困户中随机地抽取2户,求所抽到2户的满意度评分均“超过85”的概率.(参考数据:
之间,则满意度等级为“A级”.运用样本估计总体的思想,现从(1)中抽到的8个样本的满意度为“A级”贫困户中随机地抽取2户,求所抽到2户的满意度评分均“超过85”的概率.(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线C; y2 =2x的焦点为F,准线为l, P为抛物线C上异于顶点的动点.
(1)过点P作准线1的垂线,垂足为H,若△PHF与△POF的面积之比为2:1,求点P的坐标;
(2)过点M(![]() ,0)任作一条直线 m与抛物线C交于不同的两点A, B.若两直线PA, PB 斜率之和为2,求点P的坐标.
,0)任作一条直线 m与抛物线C交于不同的两点A, B.若两直线PA, PB 斜率之和为2,求点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项积为
项积为![]() ,满足
,满足![]() . 数列
. 数列![]() 的首项为
的首项为![]() ,且满足
,且满足![]() .
.
(1)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(2)记集合![]() ,若集合
,若集合![]() 的元素个数为
的元素个数为![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)是否存在正整数![]() 使得
使得![]() 成立?如果存在,请写出
成立?如果存在,请写出![]() 满足的条件,如果不存在,请说明理由.
满足的条件,如果不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,已知椭圆C:![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,右焦点F到右准线的距离为3.
,右焦点F到右准线的距离为3.
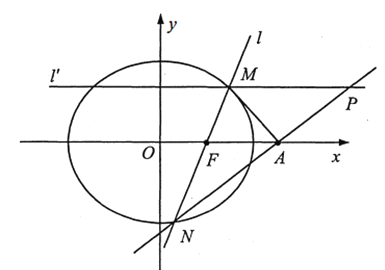
(1)求椭圆C的方程;
(2)过点F作直线l (不与x 轴重合)和椭圆C交于M, N两点,设点![]() .
.
①若![]() 的面积为
的面积为![]() ,求直线l方程;
,求直线l方程;
②过点M作与)轴垂直的直线l"和直线NA交于点P,求证:点P在一条定直线上.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校高一年级模仿《中国诗词大会》节目举办学校诗词大会,进入正赛的条件为:电脑随机抽取10首古诗,参赛者能够正确背诵6首及以上的进入正赛,若学生甲参赛,他背诵每一首古诗的正确的概率均为![]()
(1)求甲进入正赛的概率;
(2)若进入正赛,则采用积分淘汰制,规则是:电脑随机抽取4首古诗,每首古诗背诵正确加2分,错误减1分.由于难度增加,甲背诵每首古诗正确的概率为![]() ,求甲在正赛中积分
,求甲在正赛中积分![]() 的概率分布列及数学期望.
的概率分布列及数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】中国高铁的快速发展给群众出行带来巨大便利,极大促进了区域经济社会发展.已知某条高铁线路通车后,发车时间间隔![]() (单位:分钟)满足
(单位:分钟)满足![]() ,经测算,高铁的载客量与发车时间间隔
,经测算,高铁的载客量与发车时间间隔![]() 相关:当
相关:当![]() 时高铁为满载状态,载客量为
时高铁为满载状态,载客量为![]() 人;当
人;当![]() 时,载客量会在满载基础上减少,减少的人数与
时,载客量会在满载基础上减少,减少的人数与![]() 成正比,且发车时间间隔为
成正比,且发车时间间隔为![]() 分钟时的载客量为
分钟时的载客量为![]() 人.记发车间隔为
人.记发车间隔为![]() 分钟时,高铁载客量为
分钟时,高铁载客量为![]() .
.
![]() 求
求![]() 的表达式;
的表达式;
![]() 若该线路发车时间间隔为
若该线路发车时间间隔为![]() 分钟时的净收益
分钟时的净收益![]() (元),当发车时间间隔为多少时,单位时间的净收益
(元),当发车时间间隔为多少时,单位时间的净收益![]() 最大?
最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com