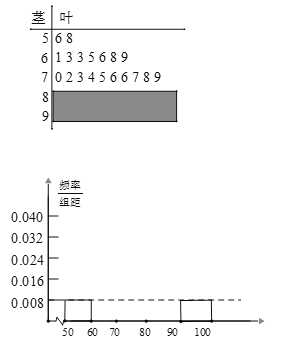
（1）完善频率分布直方图（需写出计算过程）；

（2）分别根据茎叶图和频率分布直方图求出样本数据的中位数m1和m2，并指出选用哪一个数据来估计总体的中位数更合理（需要叙述理由）．

【题目】如图所示，在四棱锥P﹣ABCD中，侧面PAD垂直底面ABCD，∠PAD＝∠ABC，设．

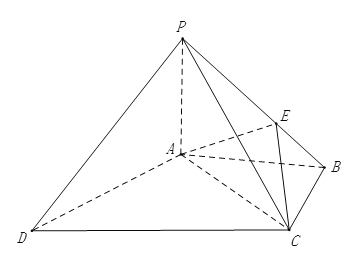
（1）求证：AE垂直BC；

（2）若直线AB∥平面PCD，且DC＝2AB，求证：直线PD∥平面ACE．

【题目】如图1，等腰梯形ABCD中，，，，O为BE中点，F为BC中点.将沿BE折起到的位置，如图2.

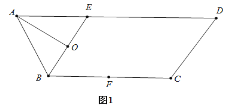
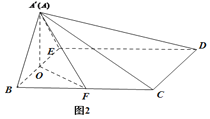
（1）证明：平面；

（2）若平面平面BCDE，求点F到平面的距离.

【题目】如图，已知是正三角形，EA，CD都垂直于平面ABC，且，二面角的平面角大小为，F是BE的中点，求证：

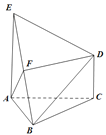
（1）平面ABC；

（2）平面EDB；

（3）求几何体的体积.

已知在平面直角坐标系中，直线的参数方程为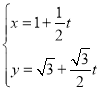（为参数），以坐标原点为极点，轴正半轴为极轴且取相同的单位长度建立极坐标系，曲线的极坐标方程为．

（1）求直线的极坐标方程与曲线的直角坐标方程；

（2）直线与曲线在第一象限交于点，直线与直线交于点，求.

【题目】已知动圆经过点，且和直线相切.

(Ⅰ)求该动圆圆心的轨迹的方程；

(Ⅱ)已知点，若斜率为1的直线与线段相交（不经过坐标原点和点），且与曲线交于两点，求面积的最大值.

【题目】通过随机询问100名性别不同的大学生是否爱好某项运动，得到如下列联表：

（1）能否有的把握认为是否爱好该项运动与性别有关？请说明理由．

（2）利用分层抽样的方法从以上爱好该项运动的大学生中抽取6人组建“运动达人社”，现从“运动达人社”中选派2人参加某项校际挑战赛，求选出的2人中恰有1名女大学生的概率．

附：

，其中

【题目】（题文）在三棱锥中，底面，，且三棱锥的每个顶点都在球的表面上，则球的表面积为 _______

【题目】已知函数有两个极值点(为自然对数的底数).

(1)求实数的取值范围;

(2)求证:

【题目】2019年春节期间，当红影视明星翟天临“不知”“知网”学术不端事件在全国闹得沸沸扬扬，引发了网友对亚洲最大电影学府北京电影学院乃至整个中国学术界高等教育乱象的反思.为进一步端正学风，打击学术造假行为，教育部日前公布的2019年部门预算中透露，2019年教育部拟抽检博士学位论文约篇，预算为万元.国务院学位委员会、教育部2014年印发的《博士硕士学位论文抽检办法》通知中规定:每篇抽检的学位论文送位同行专家进行评议，位专家中有位以上(含位)专家评议意见为“不合格”的学位论文，将认定为“存在问题学位论文”;有且只有位专家评议意见为“不合格”的学位论文，将再送位同行专家进行复评. 位复评专家中有位以上(含位)专家评议意见为“不合格”的学位论文，将认定为“存在问题学位论文”设每篇学位论文被每位专家评议为“不合格”的概率均为且各篇学位论文是否被评议为“不合格”相互独立.

(1)相关部门随机地抽查了位博士硕士的论文，每人一篇，抽检是否合格，抽检得到的部分数据如下表所示:

通过计算说明是否有的把握认为论文是否合格与作者的学位高低有关系?

(2)若，记一篇抽检的学位论文被认定为“存在问题学位论文”的概率为，求的值;

(3)若拟定每篇抽检论文不需要复评的评审费用为元，需要复评的评审费用为元;除评审费外，其他费用总计为万元现以此方案实施，且抽检论文为篇，问是否会超过预算?并说明理由.

临界值表:

参考公式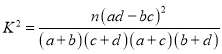,其中