
科目: 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,
,![]() ,
,![]() 为抛物线上不重合的两动点,
为抛物线上不重合的两动点,![]() 为坐标原点,
为坐标原点,![]() ,过
,过![]() ,
,![]() 作抛物线的切线
作抛物线的切线![]() ,
,![]() ,直线
,直线![]() ,
,![]() 交于点
交于点![]() .
.
(1)求抛物线的方程;
(2)问:直线![]() 是否过定点,若是,求出定点坐标,若不是,说明理由;
是否过定点,若是,求出定点坐标,若不是,说明理由;
(3)三角形![]() 的面积是否存在最小值,若存在,请求出最小值.
的面积是否存在最小值,若存在,请求出最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券,假定指针等可能地停在任一位置.若指针停在A区域返券60元;停在B区域返券30元;停在C区域不返券.例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.
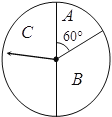
(1)若某位顾客消费128元,求返券金额不低于30元的概率;
(2)若某位顾客恰好消费280元,并按规则参与了活动,他获得返券的金额记为![]() (元).求随机变量
(元).求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,分别过椭圆![]() 左、右焦点
左、右焦点![]() 的动直线
的动直线![]() 相交于
相交于![]() 点,与椭圆
点,与椭圆![]() 分别交于
分别交于![]() 与
与![]() 不同四点,直线
不同四点,直线![]() 的斜率
的斜率![]() 满足
满足![]() , 已知
, 已知![]() 与
与![]() 轴重合时,
轴重合时, ![]() .
.
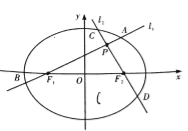
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在定点![]() 使得
使得![]() 为定值,若存在,求出
为定值,若存在,求出![]() 点坐标并求出此定值,若不存在,
点坐标并求出此定值,若不存在,
说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,倾斜角为
中,倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的倾斜角.
的倾斜角.
查看答案和解析>>
科目: 来源: 题型:
【题目】为落实国家扶贫攻坚政策,某社区应上级扶贫办的要求,对本社区所有扶贫户每年年底进行收入统计,下表是该社区扶贫户中![]() 户从2016年至2019年的收入统计数据:(其中
户从2016年至2019年的收入统计数据:(其中![]() 为
为![]() 贫困户的人均年纯收人)
贫困户的人均年纯收人)
年份 | 2016年 | 2017年 | 2018年 | 2019年 |
年份代码 |
|
|
|
|
人均纯收入 |
|
|
|
|
(1)作出贫困![]() 户的人均年纯收人的散点图;
户的人均年纯收人的散点图;
(2)根据上表数据,用最小二乘法求出![]() 关于年份代码
关于年份代码![]() 的线性回归方程
的线性回归方程![]() ,并估计
,并估计![]() 贫困户在2020年能否脱贫(注:国家规定2020年的脱贫标准:人均年纯收入不低于
贫困户在2020年能否脱贫(注:国家规定2020年的脱贫标准:人均年纯收入不低于![]() 元)
元)
(参考公式: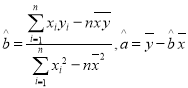 )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在直角梯形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,将
,将![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() (如图2).
(如图2).![]() 为
为![]() 中点
中点
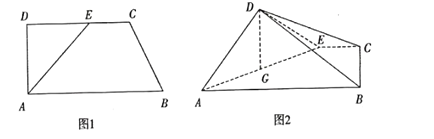
(1)求证:![]() ;
;
(2)求四棱锥![]() 的体积;
的体积;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,请说明理由
的值;若不存在,请说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com