
科目: 来源: 题型:
【题目】已知圆![]() ,直线
,直线![]() ,动圆P与圆M相外切,且与直线l相切.设动圆圆心P的轨迹为E.
,动圆P与圆M相外切,且与直线l相切.设动圆圆心P的轨迹为E.
(1)求E的方程;
(2)若点A,B是E上的两个动点,O为坐标原点,且![]() ,求证:直线AB恒过定点.
,求证:直线AB恒过定点.
查看答案和解析>>
科目: 来源: 题型:
【题目】互联网使我们的生活日益便捷,网络外卖也开始成为不少人日常生活中不可或缺的一部分,某市一调查机构针对该市市场占有率较高的甲、乙两家网络外卖企业(以下外卖甲、外卖乙)的经营情况进行了调查,调查结果如下表:
1日 | 2日 | 3日 | 4日 | 5日 | |
外卖甲日接单x(百单) | 5 | 2 | 9 | 8 | 11 |
外卖乙日接单y(百单) | 2 | 3 | 10 | 5 | 15 |
(1)试根据表格中这五天的日接单量情况,从统计的角度说明这两家外卖企业的经营状况;
(2)据统计表明,y与x之间具有线性关系.
①请用相关系数r对y与x之间的相关性强弱进行判断;(若![]() ,则可认为y与x有较强的线性相关关系(r值精确到0.001))
,则可认为y与x有较强的线性相关关系(r值精确到0.001))
②经计算求得y与x之间的回归方程为![]() ,假定每单外卖业务企业平均能获纯利润3元,试预测当外卖乙日接单量不低于25百单时,外卖甲所获取的日纯利润的大致范围.(x值精确到0.01)
,假定每单外卖业务企业平均能获纯利润3元,试预测当外卖乙日接单量不低于25百单时,外卖甲所获取的日纯利润的大致范围.(x值精确到0.01)
相关公式: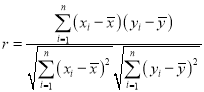 ,
,
参考数据: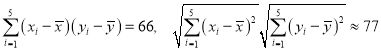 .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图的折线图是某超市2018年一月份至五月份的营业额与成本数据,根据该折线图,下列说法正确的是( )
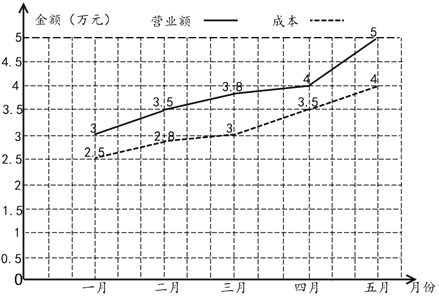
A.该超市2018年的前五个月中三月份的利润最高
B.该超市2018年的前五个月的利润一直呈增长趋势
C.该超市2018年的前五个月的利润的中位数为0.8万元
D.该超市2018年前五个月的总利润为3.5万元
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,椭圆![]() 的离心率为
的离心率为![]() ,其左焦点到椭圆上点的最远距离为3,点
,其左焦点到椭圆上点的最远距离为3,点![]() 为椭圆外一点,不过原点O的直线l与C相交于A,B两点,且线段AB被直线OP平分
为椭圆外一点,不过原点O的直线l与C相交于A,B两点,且线段AB被直线OP平分

(1)求椭圆C的标准方程
(2)求![]() 面积最大值时的直线l的方程.
面积最大值时的直线l的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() 和
和![]() 个实数
个实数![]() 若有穷数列
若有穷数列![]() 由数列
由数列![]() 的项重新排列而成,且下列条件同时成立:①
的项重新排列而成,且下列条件同时成立:① ![]() 个数
个数![]() 两两不同;②当
两两不同;②当![]() 时,
时,![]() 都成立,则称
都成立,则称![]() 为
为![]() 的一个“友数列”.
的一个“友数列”.
(1)若![]() 写出的
写出的![]() 全部“友数列”;
全部“友数列”;
(2)已知![]() 是通项公式为
是通项公式为![]() 的数列
的数列![]() 的一个“友数列”,且
的一个“友数列”,且![]() 求
求![]() (用
(用![]() 表示);
表示);
(3)设![]() 求所有使得通项公式为
求所有使得通项公式为![]() 的数列
的数列![]() 不能成为任何数列
不能成为任何数列![]() 的“友数列”的正实数
的“友数列”的正实数![]() 的个数(用
的个数(用![]() 表示).
表示).
查看答案和解析>>
科目: 来源: 题型:
【题目】设常数![]() 在平面直角坐标系
在平面直角坐标系![]() 中,已知点
中,已知点![]() 直线
直线![]() 曲线
曲线![]() 与
与![]() 轴交于点A与
轴交于点A与![]() 交于点
交于点![]() 分别是曲线
分别是曲线![]() 与线段AB上的动点.
与线段AB上的动点.
(1)用![]() 表示点B到点F的距离;
表示点B到点F的距离;
(2)若![]() 且
且![]() 求
求![]() 的值;
的值;
(3)设![]() 且存在点P、Q,使得
且存在点P、Q,使得![]() 是等边三角形,求
是等边三角形,求![]() 的边长.
的边长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某地自2014年至2019年每年年初统计所得的人口数量如下表所示:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
人数/千人 | 2082 | 2135 | 2203 | 2276 | 2339 | 2385 |
(1)根据表中的数据计算2014年至2018年每年该地人口的增长数量,并描述该地人口数量的变化趋势;
(2)研究人员用函数![]() 拟合该地的人口数量,其中
拟合该地的人口数量,其中![]() 的单位是年,2014年初对应时刻
的单位是年,2014年初对应时刻![]() 的单位是干人,设
的单位是干人,设![]() 的反函数为
的反函数为![]() 求
求![]() 的值(精确到0.1),并解释其实际意义.
的值(精确到0.1),并解释其实际意义.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在等腰![]() 中,
中,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() 为
为![]() 的中点,
的中点,![]() 在线段
在线段![]() 上,且
上,且![]() 。将
。将![]() 沿
沿![]() 折起,使点
折起,使点![]() 到
到![]() 的位置(如图2所示),且
的位置(如图2所示),且![]() 。
。
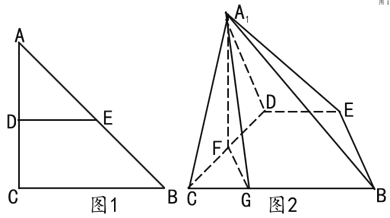
(1)证明:![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值
所成锐二面角的余弦值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com