
科目: 来源: 题型:
【题目】已知函数![]() .
.
(1)求函数![]() 的图象在点
的图象在点![]() 处的切线方程;
处的切线方程;
(2)若![]() 在
在![]() 上有解,求
上有解,求![]() 的取值范围;
的取值范围;
(3)设![]() 是函数
是函数![]() 的导函数,
的导函数,![]() 是函数
是函数![]() 的导函数,若函数
的导函数,若函数![]() 的零点为
的零点为![]() ,则点
,则点![]() 恰好就是该函数
恰好就是该函数![]() 的对称中心.试求
的对称中心.试求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某单位40岁以上的女性职工共有60人,为了调查一下体重和年龄的关系,将这60人随机按1~60编号,用系统抽样的方法从中抽取10人,测量一下体重.
(1)若被抽出的号码其中一个为7,则最后被抽出的号码是多少?
(2)被抽取的10个人的体重(单位:![]() ),用茎叶图表示如图,求这10人体重的中位数与平均数;
),用茎叶图表示如图,求这10人体重的中位数与平均数;

(3)从这10个人中体重超过![]() 的人中随机抽取2人,参加健康指导培训,求体重为
的人中随机抽取2人,参加健康指导培训,求体重为![]() 的人被抽到的概率.
的人被抽到的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() 的最小值为-2,
的最小值为-2,![]() 的图象的相邻两条对称轴之间的距离为
的图象的相邻两条对称轴之间的距离为![]() ,
,![]() 的图象过点
的图象过点![]() .
.
(1)求函数![]() 的解析式和单调递增区间;
的解析式和单调递增区间;
(2)若![]() 函数
函数![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目: 来源: 题型:
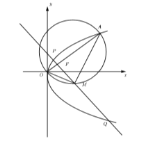
【题目】如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 的焦点为
的焦点为![]() ,
,![]() 为抛物线上异于原点的任意一点,以
为抛物线上异于原点的任意一点,以![]() 为直径作圆
为直径作圆![]() ,当直线
,当直线![]() 的斜率为1时,
的斜率为1时,![]() .
.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)过焦点![]() 作
作![]() 的垂线
的垂线![]() 与圆
与圆![]() 的一个交点为
的一个交点为![]() ,
,![]() 交抛物线于
交抛物线于![]() ,
,![]() (点
(点![]() 在点
在点![]() ,
,![]() 之间),记
之间),记![]() 的面积为
的面积为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某省从2021年开始将全面推行新高考制度,新高考“![]() ”中的“2”要求考生从政治、化学、生物、地理四门中选两科,按照等级赋分计入高考成绩,等级赋分规则如下:从2021年夏季高考开始,高考政治、化学、生物、地理四门等级考试科目的考生原始成绩从高到低划分为
”中的“2”要求考生从政治、化学、生物、地理四门中选两科,按照等级赋分计入高考成绩,等级赋分规则如下:从2021年夏季高考开始,高考政治、化学、生物、地理四门等级考试科目的考生原始成绩从高到低划分为![]() 五个等级,确定各等级人数所占比例分别为
五个等级,确定各等级人数所占比例分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,等级考试科目成绩计入考生总成绩时,将
,等级考试科目成绩计入考生总成绩时,将![]() 至
至![]() 等级内的考生原始成绩,依照等比例转换法分别转换到
等级内的考生原始成绩,依照等比例转换法分别转换到![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五个分数区间,得到考生的等级分,等级转换分满分为100分.具体转换分数区间如下表:
五个分数区间,得到考生的等级分,等级转换分满分为100分.具体转换分数区间如下表:
等级 |
|
|
|
|
|
比例 |
|
|
|
|
|
赋分区间 |
|
|
|
|
|
而等比例转换法是通过公式计算:![]()
其中![]() ,
,![]() 分别表示原始分区间的最低分和最高分,
分别表示原始分区间的最低分和最高分,![]() 、
、![]() 分别表示等级分区间的最低分和最高分,
分别表示等级分区间的最低分和最高分,![]() 表示原始分,
表示原始分,![]() 表示转换分,当原始分为
表示转换分,当原始分为![]() ,
,![]() 时,等级分分别为
时,等级分分别为![]() 、
、![]()
假设小南的化学考试成绩信息如下表:
考生科目 | 考试成绩 | 成绩等级 | 原始分区间 | 等级分区间 |
化学 | 75分 |
|
|
|
设小南转换后的等级成绩为![]() ,根据公式得:
,根据公式得:![]() ,
,
所以![]() (四舍五入取整),小南最终化学成绩为77分.
(四舍五入取整),小南最终化学成绩为77分.
已知某年级学生有100人选了化学,以半期考试成绩为原始成绩转换本年级的化学等级成绩,其中化学成绩获得![]() 等级的学生原始成绩统计如下表:
等级的学生原始成绩统计如下表:
成绩 | 95 | 93 | 91 | 90 | 88 | 87 | 85 |
人数 | 1 | 2 | 3 | 2 | 3 | 2 | 2 |
(1)从化学成绩获得![]() 等级的学生中任取2名,求恰好有1名同学的等级成绩不小于96分的概率;
等级的学生中任取2名,求恰好有1名同学的等级成绩不小于96分的概率;
(2)从化学成绩获得![]() 等级的学生中任取5名,设5名学生中等级成绩不小于96分人数为
等级的学生中任取5名,设5名学生中等级成绩不小于96分人数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】某网店经营的一种商品进行进价是每件10元,根据一周的销售数据得出周销售量![]() (件)与单价
(件)与单价![]() (元)之间的关系如下图所示,该网店与这种商品有关的周开支均为25元.
(元)之间的关系如下图所示,该网店与这种商品有关的周开支均为25元.

(1)根据周销售量图写出![]() (件)与单价
(件)与单价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)写出利润![]() (元)与单价
(元)与单价![]() (元)之间的函数关系式;当该商品的销售价格为多少元时,周利润最大?并求出最大周利润.
(元)之间的函数关系式;当该商品的销售价格为多少元时,周利润最大?并求出最大周利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com