
科目: 来源: 题型:
【题目】某贫困村共有农户100户,均从事水果种植,平均每户年收入为1.8万元,在当地政府大力扶持和引导下,村委会决定2020年初抽出![]() 户(
户(![]() ,
,![]() )从事水果销售工作,经测算,剩下从事水果种植的农户平均每户年收入比上一年提高了
)从事水果销售工作,经测算,剩下从事水果种植的农户平均每户年收入比上一年提高了![]() ,而从事水果销售的农户平均每户年收入为
,而从事水果销售的农户平均每户年收入为![]() 万元.
万元.
(1)为了使从事水果种植的农户三年后平均每户年收入不低于2.4万元,那么2020年初至少应抽出多少农户从事水果销售工作?
(2)若一年后,该村平均每户的年收入为![]() (万元),问
(万元),问![]() 的最大值是否可以达到2.1万元?
的最大值是否可以达到2.1万元?
查看答案和解析>>
科目: 来源: 题型:
【题目】商品的销售价格与销售量密切相关,为更精准地为商品确定最终售价,商家对商品A按以下单价进行试售,得到部分的数据如下:
单价 |
|
|
|
|
|
销量 |
|
|
|
|
|
(1)求销量![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)预计今后的销售中,销量与单价服从(1)中的线性回归方程,已知每件商品![]() 的成本是
的成本是![]() 元,为了获得最大利润,商品
元,为了获得最大利润,商品![]() 的单价应定为多少元?(结果保留整数)
的单价应定为多少元?(结果保留整数)
参考数据:![]() ,
,![]() ,
,![]() )(参考公式:
)(参考公式: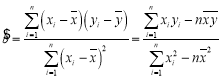 ,
,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程:在直角坐标系![]() 中,曲线
中,曲线![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)已知点![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() ,它与曲线
,它与曲线![]() 的交点为
的交点为![]() ,
,![]() ,与曲线
,与曲线![]() 的交点为
的交点为![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】设椭圆![]() ,离心率
,离心率![]() ,短轴
,短轴![]() ,抛物线顶点在原点,以坐标轴为对称轴,焦点为
,抛物线顶点在原点,以坐标轴为对称轴,焦点为![]() ,
,
(1)求椭圆和抛物线的方程;
(2)设坐标原点为![]() ,
,![]() 为抛物线上第一象限内的点,
为抛物线上第一象限内的点,![]() 为椭圆是一点,且有
为椭圆是一点,且有![]() ,当线段
,当线段![]() 的中点在
的中点在![]() 轴上时,求直线
轴上时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知四边形![]() 为矩形,
为矩形, ![]() ,
,![]() 为
为![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起,得到四棱锥
折起,得到四棱锥![]() ,设
,设![]() 的中点为
的中点为![]() ,在翻折过程中,得到如下有三个命题:
,在翻折过程中,得到如下有三个命题:
①![]() 平面
平面![]() ,且
,且![]() 的长度为定值
的长度为定值![]() ;
;
②三棱锥![]() 的最大体积为
的最大体积为![]() ;
;
③在翻折过程中,存在某个位置,使得![]() .
.
其中正确命题的序号为__________.(写出所有正确结论的序号)
查看答案和解析>>
科目: 来源: 题型:
【题目】若数列![]() 同时满足条件:①存在互异的
同时满足条件:①存在互异的![]() 使得
使得![]() (
(![]() 为常数);
为常数);
②当![]() 且
且![]() 时,对任意
时,对任意![]() 都有
都有![]() ,则称数列
,则称数列![]() 为双底数列.
为双底数列.
(1)判断以下数列![]() 是否为双底数列(只需写出结论不必证明);
是否为双底数列(只需写出结论不必证明);
①![]() ; ②
; ②![]() ; ③
; ③![]()
(2)设![]() ,若数列
,若数列![]() 是双底数列,求实数
是双底数列,求实数![]() 的值以及数列
的值以及数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)设![]() ,是否存在整数
,是否存在整数![]() ,使得数列
,使得数列![]() 为双底数列?若存在,求出所有的
为双底数列?若存在,求出所有的![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com