【题目】在平面直角坐标系中，已知曲线的参数方程为（为参数），以坐标原点为极点，以轴的正半轴为极轴，建立极坐标系，曲线的极坐标方程为.

（1）设点分别为曲线与曲线上的任意一点，求的最大值；

（2）设直线（为参数）与曲线交于两点，且，求直线的普通方程.

【题目】峰谷电是目前在城市居民当中开展的一种电价类别．它是将一天24小时划分成两个时间段，把8：00—22：00共14小时称为峰段，执行峰电价，即电价上调；22：00—次日8：00共10个小时称为谷段，执行谷电价，即电价下调．为了进一步了解民众对峰谷电价的使用情况，从某市一小区随机抽取了50 户住户进行夏季用电情况调查，各户月平均用电量以，，，，，（单位：度）分组的频率分布直方图如下图：

若将小区月平均用电量不低于700度的住户称为“大用户”，月平均用电量低于700度的住户称为“一般用户”．其中，使用峰谷电价的户数如下表：

(1)估计所抽取的 50户的月均用电量的众数和平均数（同一组中的数据用该组区间的中点值作代表）；

(2)（）将“一般用户”和“大用户”的户数填入下面的列联表:

()根据（）中的列联表，能否有的把握认为 “用电量的高低”与“使用峰谷电价”有关？

附：，

【题目】已知函数.

（1）讨论的单调性；

（2）若，试判断的零点个数.

【题目】设椭圆的左焦点为，离心率为，为圆的圆心.

（1）求椭圆的方程；

（2）已知过椭圆右焦点的直线交椭圆于两点，过且与垂直的直线与圆交于两点，求四边形面积的取值范围.

【题目】已知曲线C的极坐标方程是ρ＝6sinθ，建立以极点为坐标原点，极轴为x轴正半轴的平面直角坐标系．直线l的参数方程是，(t为参数)．

(1)求曲线C的直角坐标方程；

(2)若直线l与曲线C相交于A，B两点，且|AB|=，求直线的斜率k．

【题目】已知抛物线，的焦点为，过点的直线的斜率为，与抛物线交于，两点，抛物线在点，处的切线分别为，，两条切线的交点为．

（1）证明：；

（2）若的外接圆与抛物线有四个不同的交点，求直线的斜率的取值范围．

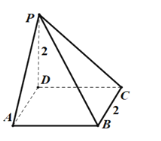
(1)求该四棱锥P-ABCD的表面积和体积；

(2)求该四棱锥P-ABCD内切球的表面积.

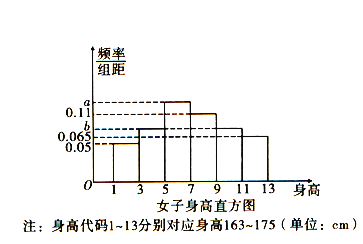
(1)求直方图中a，b的值；

(2)估计这个阵营女子身高的平均值 (同一组中的数据用该组区间的中点值为代表)

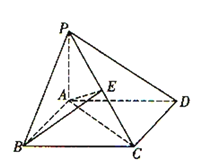
下列四个结论：①AB⊥AC；②AB⊥平面PAC；③PC⊥平面ABE；④BE⊥PC．正确的个数是( )

A.1B.2C.3D.4

A.n=360，m=14B.n=420，m=15C.n=540，m=18D.n=660，m=19