
科目: 来源: 题型:
【题目】已知正项数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若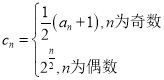
![]() ,从数列
,从数列![]() 中抽出部分项(奇数项与偶数项均不少于两项),将抽出的项按照某一顺序排列后构成等差数列.当等差数列的项数最大时,求所有满足条件的等差数列.
中抽出部分项(奇数项与偶数项均不少于两项),将抽出的项按照某一顺序排列后构成等差数列.当等差数列的项数最大时,求所有满足条件的等差数列.
查看答案和解析>>
科目: 来源: 题型:
【题目】某公园为了美化环境和方便顾客,计划建造一座圆弧形拱桥,已知该桥的剖面如图所示,共包括圆弧形桥面![]() 和两条长度相等的直线型路面
和两条长度相等的直线型路面![]() 、
、![]() ,桥面跨度
,桥面跨度![]() 的长不超过
的长不超过![]() 米,拱桥
米,拱桥![]() 所在圆的半径为
所在圆的半径为![]() 米,圆心
米,圆心![]() 在水面
在水面![]() 上,且
上,且![]() 和
和![]() 所在直线与圆
所在直线与圆![]() 分别在连结点
分别在连结点![]() 和
和![]() 处相切.设
处相切.设![]() ,已知直线型桥面每米修建费用是
,已知直线型桥面每米修建费用是![]() 元,弧形桥面每米修建费用是
元,弧形桥面每米修建费用是![]() 元.
元.
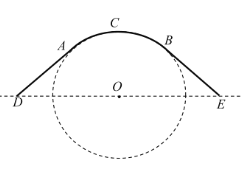
(1)若桥面(线段![]() 、
、![]() 和弧
和弧![]() )的修建总费用为
)的修建总费用为![]() 元,求
元,求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)当![]() 为何值时,桥面修建总费用
为何值时,桥面修建总费用![]() 最低?
最低?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数集![]() (
(![]() ,
,![]() )具有性质
)具有性质![]() :对任意的
:对任意的![]() 、
、![]() (
(![]() ),
),![]() 与
与![]() 两数中至少有一个属于
两数中至少有一个属于![]() .
.
(1)分别判断数集![]() 与
与![]() 是否具有性质
是否具有性质![]() ,并说明理由;
,并说明理由;
(2)证明:![]() ,且
,且![]() ;
;
(3)证明:当![]() 时,
时,![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 成等比数列.
成等比数列.
查看答案和解析>>
科目: 来源: 题型:
【题目】由于浓酸泄漏对河流形成了污染,现决定向河中投入固体碱,1个单位的固体碱在水中逐步溶化,水中的碱浓度![]() 与时间
与时间![]() 的关系,可近似地表示为
的关系,可近似地表示为 ,只有当河流中碱的浓度不低于1时,才能对污染产生有效的抑制作用.
,只有当河流中碱的浓度不低于1时,才能对污染产生有效的抑制作用.
(1)如果只投放1个单位的固体碱,则能够维持有效抑制作用的时间有多长?
(2)当河中的碱浓度开始下降时,即刻第二次投放1个单位的固体碱,此后,每一时刻河中的碱浓度认为是各次投放的碱在该时刻相应的碱浓度的和,求河中碱浓度可能取得的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】记方程①x2+a1x+1=0,②x2+a2x+1=0,③x2+a3x+1=0,其中a1,a2,a3是正实数,当a1,a2,a3成等比数列,下列选项中,当方程③有实根时,能推出的是( )
A.方程①有实根或方程②无实根B.方程①有实根或方程②有实根
C.方程①无实根或方程②无实根D.方程①无实根或方程②有实根
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的左、右两个顶点分别为
的左、右两个顶点分别为![]() 、
、![]() ,曲线
,曲线![]() 是以
是以![]() 、
、![]() 两点为顶点,焦距为
两点为顶点,焦距为![]() 的双曲线,设点
的双曲线,设点![]() 在第一象限且在曲线
在第一象限且在曲线![]() 上,直线
上,直线![]() 与椭圆相交于另一点
与椭圆相交于另一点![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)设![]() 、
、![]() 两点的横坐标分别为
两点的横坐标分别为![]() 、
、![]() ,求证
,求证![]() 为一定值;
为一定值;
(3)设△![]() 与△
与△![]() (其中
(其中![]() 为坐标原点)的面积分别为
为坐标原点)的面积分别为![]() 与
与![]() ,且
,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com