【题目】业界称“中国芯”迎来发展和投资元年，某芯片企业准备研发一款产品，研发启动时投入资金为(为常数)元,之后每年会投入一笔研发资金,年后总投入资金记为,经计算发现当时,近似地满足，其中为常数,.已知年后总投入资金为研发启动时投入资金的倍．问

（1）研发启动多少年后,总投入资金是研发启动时投入资金的倍;

（2）研发启动后第几年的投入资金的最多.

【题目】已知函数，.

（1）若函数有且只有两个零点，求实数的取值范围；

（2）设函数的两个零点为，，且，求证.

【题目】在平面直角坐标系xOy中，曲线C的参数方程为(α为参数)，在以坐标原点O为极点，x轴的正半轴为极轴的极坐标系中，点P的极坐标为，直线l的极坐标方程为.

(1)求直线l的直角坐标方程与曲线C的普通方程；

(2)若Q是曲线C上的动点，M为线段PQ的中点，直线l上有两点A，B，始终满足|AB|＝4，求△MAB面积的最大值与最小值.

(1)求取出的4个球中恰有1个红球的概率；

(2)设ξ为取出的4个球中红球的个数，求ξ的分布列和数学期望.

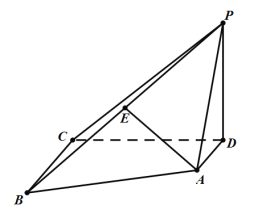
(1)求证：AE//平面PDC；

(2)若BC＝CD＝PD，求直线AC与平面PBC所成角的余弦值.

【题目】设P为椭圆1（a＞b＞0）上任一点，F1、F2为椭圆的焦点，|PF1|+|PF2|＝4，离心率为．

（1）求椭圆的方程；

（2）若直线l：y＝kx+m（≠0）与椭圆交于A、B两点，若线段AB的中点C的直线yx上，O为坐标原点．求△OAB的面积S的最大值．

【题目】已知函数，

（1）求f（x）的单调递增区间；

（2）设△ABC的三个内角A，B，C的对边分别为a，b，c，若且a＝2时，求△ABC周长的最大值．

（1）求数列{an}的通项公式；

（2）设数列{bn}满足，求数列{bn}的前n项和Sn．

【题目】在直角坐标系中，直线l的参数方程为(t为参数，)，以坐标原点为极点，轴正半轴为极轴，取相同的长度单位建立极坐标系，曲线C的极坐标方程为.

(1)当时，写出直线l的普通方程及曲线C的直角坐标方程；

(2)已知点，设直线l与曲线C交于A，B两点，试确定的取值范围．

【题目】已知函数.

（1）求的单调区间；

（2）若，求的取值范围.