
科目: 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,椭圆的离心率为
,椭圆的离心率为![]() ,过椭圆
,过椭圆![]() 的左焦点
的左焦点![]() ,且斜率为
,且斜率为![]() 的直线
的直线![]() ,与以右焦点
,与以右焦点![]() 为圆心,半径为
为圆心,半径为![]() 的圆
的圆![]() 相切.
相切.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)线段![]() 是椭圆
是椭圆![]() 过右焦点
过右焦点![]() 的弦,且
的弦,且![]() ,求
,求![]() 的面积的最大值以及取最大值时实数
的面积的最大值以及取最大值时实数![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,菱形ABCD的边长为a,∠D=60°,点H为DC边中点,现以线段AH为折痕将△DAH折起使得点D到达点P的位置且平面PHA⊥平面ABCH,点E,F分别为AB,AP的中点.
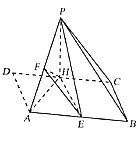
(1)求证:平面PBC∥平面EFH;
(2)若三棱锥P﹣EFH的体积等于![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某次高三年级模拟考试中,数学试卷有一道满分10分的选做题,学生可以从A,B两道题目中任选一题作答.某校有900名高三学生参加了本次考试,为了了解该校学生解答该选做题的得分情况,作为下一步教学的参考依据,计划从900名考生的选做题成绩中随机抽取一个容量为10的样本,为此将900名考生选做题的成绩按照随机顺序依次编号为001~900.
(1)若采用系统抽样法抽样,从编号为001~090的成绩中用简单随机抽样确定的成绩编号为025,求样本中所有成绩编号之和;
(2)若采用分层抽样,按照学生选择A题目或B题目,将成绩分为两层.已知该校高三学生有540人选做A题目,有360人选做B题目,选取的样本中,A题目的成绩平均数为5,方差为2,B题目的成绩平均数为5.5,方差为0.25.
(i)用样本估计该校这900名考生选做题得分的平均数与方差;
(ii)本选做题阅卷分值都为整数,且选取的样本中,A题目成绩的中位数和B题目成绩的中位数都是5.5.从样本中随机选取两个大于样本平均值的数据做进一步调查,求取到的两个成绩来自不同题目的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,椭圆的离心率为
,椭圆的离心率为![]() ,过椭圆
,过椭圆![]() 的左焦点
的左焦点![]() ,且斜率为
,且斜率为![]() 的直线
的直线![]() ,与以右焦点
,与以右焦点![]() 为圆心,半径为
为圆心,半径为![]() 的圆
的圆![]() 相切.
相切.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)线段![]() 是椭圆
是椭圆![]() 过右焦点
过右焦点![]() 的弦,且
的弦,且![]() ,求
,求![]() 的面积的最大值以及取最大值时实数
的面积的最大值以及取最大值时实数![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】随着科技的发展,网络已逐渐融入了人们的生活.网购是非常方便的购物方式,为了了解网购在我市的普及情况,某调查机构进行了有关网购的调查问卷,并从参与调查的市民中随机抽取了男女各100人进行分析,从而得到表(单位:人)
经常网购 | 偶尔或不用网购 | 合计 | |
男性 | 50 | 100 | |
女性 | 70 | 100 | |
合计 |
(1)完成上表,并根据以上数据判断能否在犯错误的概率不超过0.01的前提下认为我市市民网购与性别有关?
(2)①现从所抽取的女市民中利用分层抽样的方法抽取10人,再从这10人中随机选取3人赠送优惠券,求选取的3人中至少有2人经常网购的概率;
②将频率视为概率,从我市所有参与调查的市民中随机抽取10人赠送礼品,记其中经常网购的人数为![]() ,求随机变量
,求随机变量![]() 的数学期望和方差.
的数学期望和方差.
参考公式: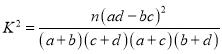
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】为响应绿色出行,某市在推出“共享单车”后,又推出“新能源分时租赁汽车”.其中一款新能源分时租赁汽车,每次租车收费的标准由两部分组成:①根据行驶里程数按1元/公里计费;②行驶时间不超过![]() 分时,按
分时,按![]() 元/分计费;超过
元/分计费;超过![]() 分时,超出部分按
分时,超出部分按![]() 元/分计费.已知王先生家离上班地点
元/分计费.已知王先生家离上班地点![]() 公里,每天租用该款汽车上、下班各一次.由于堵车、红绿灯等因素,每次路上开车花费的时间
公里,每天租用该款汽车上、下班各一次.由于堵车、红绿灯等因素,每次路上开车花费的时间 ![]() (分)是一个随机变量.现统计了
(分)是一个随机变量.现统计了![]() 次路上开车花费时间,在各时间段内的频数分布情况如下表所示:
次路上开车花费时间,在各时间段内的频数分布情况如下表所示:
时间 |
|
|
|
|
频数 |
|
|
|
|
将各时间段发生的频率视为概率,每次路上开车花费的时间视为用车时间,范围为![]() 分.(1)写出王先生一次租车费用
分.(1)写出王先生一次租车费用![]() (元)与用车时间
(元)与用车时间![]() (分)的函数关系式;(2)若王先生一次开车时间不超过
(分)的函数关系式;(2)若王先生一次开车时间不超过![]() 分为“路段畅通”,设
分为“路段畅通”,设![]() 表示3次租用新能源分时租赁汽车中“路段畅通”的次数,求的分布列和期望.
表示3次租用新能源分时租赁汽车中“路段畅通”的次数,求的分布列和期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com