
科目: 来源: 题型:
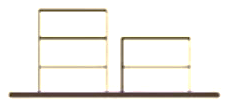
【题目】如图,在地上有同样大小的 5 块积木,一堆 2 个,一堆 3 个,要把积木一块一块的全部放到某个盒子里,每次 只能取出其中一堆最上面的一块,则不同的取法有______种(用数字作答).
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的极坐标方程;
的极坐标方程;
(2)将曲线![]() 上所有点的横坐标不变,纵坐标缩短到原来的
上所有点的横坐标不变,纵坐标缩短到原来的![]() 倍,得到曲线
倍,得到曲线![]() ,若
,若![]() 与
与![]() 的交点为
的交点为![]() (异于坐标原点
(异于坐标原点![]() ),
),![]() 与
与![]() 的交点为
的交点为![]() ,求
,求![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】某种产品的质量用其质量指标值来衡量)质量指标值越大表明质量越好,且质量指标值大于或等于102的产品为优质品.现用两种新配方(分别称为![]() 配方和
配方和![]() 配方)做试验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
配方)做试验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
![]() 配方的频数分布表:
配方的频数分布表:
指标值分组 | [90,94) | [94,98) | [98,102) | [102,106) | [106,110] |
频数 | 8 | 20 | 42 | 22 | 8 |
![]() 配方的频数分布表:
配方的频数分布表:
指标值分组 | [90,94) | [94,98) | [98,102) | [102,106] | [106,110] |
频数 | 4 | 12 | 42 | 32 | 10 |
(1)分别估计用![]() 配方、
配方、![]() 配方生产的产品的优质品率;
配方生产的产品的优质品率;
(2)已知用![]() 配方生产的一件产品的利润(单位:元)与其质量指标值
配方生产的一件产品的利润(单位:元)与其质量指标值![]() 的关系为
的关系为 ,估计用
,估计用![]() 配方生产的一件产品的利润大于
配方生产的一件产品的利润大于![]() 的概率,并求用
的概率,并求用![]() 配方生产的上述
配方生产的上述![]() 件产品的平均利润.
件产品的平均利润.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和
项和![]() 满足
满足![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)记![]() ,
,![]() 是数列
是数列![]() 的前
的前![]() 项和,若对任意的
项和,若对任意的![]() ,不等式
,不等式![]() 都成立,求实数
都成立,求实数![]() 的取值范围;
的取值范围;
(3)记![]() ,是否存在互不相等的正整数
,是否存在互不相等的正整数![]() ,
,![]() ,
,![]() ,使
,使![]() ,
,![]() ,
,![]() 成等差数列,且
成等差数列,且![]() ,
,![]() ,
,![]() 成等比数列?如果存在,求出所有符合条件的
成等比数列?如果存在,求出所有符合条件的![]() ,
,![]() ,
,![]() ;如果不存在,请说明理由.
;如果不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知直线![]() 为椭圆
为椭圆![]() 的右准线,直线
的右准线,直线![]() 与
与![]() 轴的交点记为
轴的交点记为![]() ,过右焦点
,过右焦点![]() 的直线与椭圆交于
的直线与椭圆交于![]() ,
,![]() 两点.
两点.
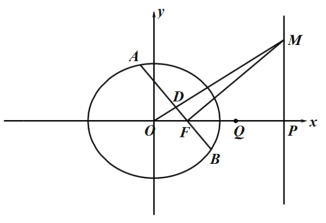
(1)设点![]() 在直线上,且满足
在直线上,且满足![]() ,若直线
,若直线![]() 与线段
与线段![]() 交于点
交于点![]() ,求证:点
,求证:点![]() 为线段
为线段![]() 的中点;
的中点;
(2)设![]() 点的坐标为
点的坐标为![]() ,直线
,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,试问
,试问![]() 是否为定值,若是,求出这个定值,若不是,请说明理由.
是否为定值,若是,求出这个定值,若不是,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某沿海特区为了缓解建设用地不足的矛盾,决定进行围海造陆以增加陆地面积.如图,两海岸线![]() ,
,![]() 所成角为
所成角为![]() ,现欲在海岸线
,现欲在海岸线![]() ,
,![]() 上分别取点
上分别取点![]() ,
,![]() 修建海堤,以便围成三角形陆地
修建海堤,以便围成三角形陆地![]() ,已知海堤
,已知海堤![]() 长为6千米.
长为6千米.
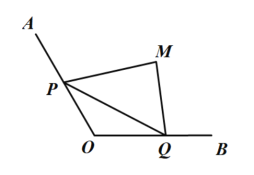
(1)如何选择![]() ,
,![]() 的位置,使得
的位置,使得![]() 的面积最大;
的面积最大;
(2)若需要进一步扩大围海造陆工程,在海堤![]() 的另一侧选取点
的另一侧选取点![]() ,修建海堤
,修建海堤![]() ,
,![]() 围成四边形陆地.当海堤
围成四边形陆地.当海堤![]() 与
与![]() 的长度之和为10千米时,求四边形
的长度之和为10千米时,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】“移动支付、高铁、网购、共享单车”被称为中国的“新四大发明”.为了帮助50岁以上的中老年人更快地适应“移动支付”,某机构通过网络组织50岁以上的中老年人学习移动支付相关知识.学习结束后,每人都进行限时答卷,得分都在![]() 内.在这些答卷(有大量答卷)中,随机抽出
内.在这些答卷(有大量答卷)中,随机抽出![]() 份,统计得分绘出频率分布直方图如图.
份,统计得分绘出频率分布直方图如图.
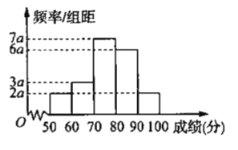
(1)求出图中![]() 的值,并求样本中,答卷成绩在
的值,并求样本中,答卷成绩在![]() 上的人数;
上的人数;
(2)以样本的频率为概率,从参加这次答卷的人群中,随机抽取![]() 名,记成绩在
名,记成绩在![]() 分以上(含
分以上(含![]() 分)的人数为
分)的人数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知无穷数列![]() 的各项都是正数,其前
的各项都是正数,其前![]() 项和为
项和为![]() ,且满足:
,且满足:![]() ,
,![]() ,其中
,其中![]() ,常数
,常数![]()
![]() .
.
(1)求证:![]() 是一个定值;
是一个定值;
(2)若数列![]() 是一个周期数列(存在正整数
是一个周期数列(存在正整数![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 为周期数列,
为周期数列,![]() 为它的一个周期),求该数列的最小周期;
为它的一个周期),求该数列的最小周期;
(3)若数列![]() 是各项均为有理数的等差数列,
是各项均为有理数的等差数列,![]() (
(![]() ),问:数列
),问:数列![]() 中的所有项是否都是数列
中的所有项是否都是数列![]() 中的项?若是,请说明理由;若不是,请举出反例.
中的项?若是,请说明理由;若不是,请举出反例.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() ,
,![]() ,求
,求![]() 的值域;
的值域;
(2)当![]() 时,求
时,求![]() 的最小值
的最小值![]() ;
;
(3)是否存在实数![]() 、
、![]() ,同时满足下列条件:①
,同时满足下列条件:① ![]() ;② 当
;② 当![]() 的定义域为
的定义域为![]() 时,其值域为
时,其值域为![]() .若存在,求出
.若存在,求出![]() 、
、![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com