
科目: 来源: 题型:
【题目】根据某省的高考改革方案,考生应在3门理科学科(物理、化学、生物)和3门文科学科(历史、政治、地理)的6门学科中选择3门学科参加考试.根据以往统计资料,1位同学选择生物的概率为0.5,选择物理但不选择生物的概率为0.2,考生选择各门学科是相互独立的.
(1)求1位考生至少选择生物、物理两门学科中的1门的概率;
(2)某校高二段400名学生中,选择生物但不选择物理的人数为140,求1位考生同时选择生物、物理两门学科的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系上,有一点列![]() ,设点
,设点![]() 的坐标
的坐标![]() (
(![]() ),其中
),其中![]() . 记
. 记![]() ,
,![]() ,且满足
,且满足![]() (
(![]() ).
).
(1)已知点![]() ,点
,点![]() 满足
满足![]() ,求
,求![]() 的坐标;
的坐标;
(2)已知点![]() ,
,![]() (
(![]() ),且
),且![]() (
(![]() )是递增数列,点
)是递增数列,点![]() 在直线
在直线![]() :
:![]() 上,求
上,求![]() ;
;
(3)若点![]() 的坐标为
的坐标为![]() ,
,![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
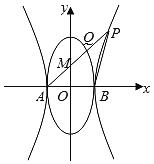
【题目】如图,椭圆![]() 的左、右顶点分别为A、B,双曲线
的左、右顶点分别为A、B,双曲线![]() 以A、B为顶点,焦距为
以A、B为顶点,焦距为![]() ,点P是
,点P是![]() 上在第一象限内的动点,直线AP与椭圆相交于另一点Q,线段AQ的中点为M,记直线AP的斜率为
上在第一象限内的动点,直线AP与椭圆相交于另一点Q,线段AQ的中点为M,记直线AP的斜率为![]()
![]() 为坐标原点.
为坐标原点.
(1)求双曲线![]() 的方程;
的方程;
(2)求点M的纵坐标![]() 的取值范围;
的取值范围;
(3)是否存在定直线![]() 使得直线BP与直线OM关于直线
使得直线BP与直线OM关于直线![]() 对称?若存在,求直线
对称?若存在,求直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
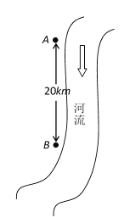
【题目】如图所示,沿河有A、B两城镇,它们相距![]() 千米.以前,两城镇的污水直接排入河里,现为保护环境,污水需经处理才能排放.两城镇可以单独建污水处理厂,或者联合建污水处理厂(在两城镇之间或其中一城镇建厂,用管道将污水从各城镇向污水处理厂输送).依据经验公式,建厂的费用为
千米.以前,两城镇的污水直接排入河里,现为保护环境,污水需经处理才能排放.两城镇可以单独建污水处理厂,或者联合建污水处理厂(在两城镇之间或其中一城镇建厂,用管道将污水从各城镇向污水处理厂输送).依据经验公式,建厂的费用为![]() (万元),
(万元),![]() 表示污水流量;铺设管道的费用(包括管道费)
表示污水流量;铺设管道的费用(包括管道费)![]() (万元),
(万元),![]() 表示输送污水管道的长度(千米).已知城镇A和城镇B的污水流量分别为
表示输送污水管道的长度(千米).已知城镇A和城镇B的污水流量分别为![]() 、
、![]() ,
,![]() 、
、![]() 两城镇连接污水处理厂的管道总长为
两城镇连接污水处理厂的管道总长为![]() 千米.假定:经管道输送的污水流量不发生改变,污水经处理后直接排入河中.请解答下列问题(结果精确到
千米.假定:经管道输送的污水流量不发生改变,污水经处理后直接排入河中.请解答下列问题(结果精确到![]() ):
):
(1)若在城镇A和城镇B单独建厂,共需多少总费用?
(2)考虑联合建厂可能节约总投资,设城镇A到拟建厂的距离为![]() 千米,求联合建厂的总费用
千米,求联合建厂的总费用![]() 与
与![]() 的函数关系式,并求
的函数关系式,并求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,如果存在给定的实数对
,如果存在给定的实数对![]() ,使得
,使得![]() 恒成立,则称
恒成立,则称![]() 为“
为“![]() 函数”;
函数”;
(1)判断函数![]() ,
,![]() 是否是“
是否是“![]() 函数”;
函数”;
(2)若![]() 是一个“
是一个“![]() 函数”,求出所有满足条件的有序实数对
函数”,求出所有满足条件的有序实数对![]() ;
;
(3)若定义域为![]() 的函数
的函数![]() 是“
是“![]() 函数”,且存在满足条件的有序实数对
函数”,且存在满足条件的有序实数对![]() 和
和![]() ,当
,当![]() 时,
时,![]() 的值域为
的值域为![]() ,求当
,求当![]() 时
时![]() 的值域;
的值域;
查看答案和解析>>
科目: 来源: 题型:
【题目】某环境保护部门对某处的环境状况用“污染指数”来监测,据测定,该处的“污染指数”与附近污染源的强度和距离之比成正比,比例系数为常数![]()
![]() ,现已知相距
,现已知相距![]() 的
的![]() 两家化工厂(污染源)的污染强度分别为1和
两家化工厂(污染源)的污染强度分别为1和![]()
![]() ,它们连线段上任意一点
,它们连线段上任意一点![]() 处的污染指数
处的污染指数![]() 等于两化工厂对该处的污染指数之和,设
等于两化工厂对该处的污染指数之和,设![]() ;
;
(1)试将![]() 表示为
表示为![]() 的函数,指出其定义域;
的函数,指出其定义域;
(2)当![]() 时,
时,![]() 处的“污染指数”最小,试求
处的“污染指数”最小,试求![]() 化工厂的污染强度
化工厂的污染强度![]() 的值;
的值;
查看答案和解析>>
科目: 来源: 题型:
【题目】在集合![]() 的子集中选出4个不同的子集,需同时满足以下两个条件:
的子集中选出4个不同的子集,需同时满足以下两个条件:
(1)![]() ,
,![]() 都要选出;(2)对选出的任意两个子集
都要选出;(2)对选出的任意两个子集![]() 和
和![]() ,必有
,必有![]() 或
或![]() ;
;
那么具有_______种不同的选法;
查看答案和解析>>
科目: 来源: 题型:
【题目】某花圃为提高某品种花苗质量,开展技术创新活动,在![]() ,
,![]() 实验地分别用甲、乙方法培育该品种花苗.为观测其生长情况,分别在
实验地分别用甲、乙方法培育该品种花苗.为观测其生长情况,分别在![]() ,
,![]() 试验地随机抽选各
试验地随机抽选各![]() 株,对每株进行综合评分(评分的高低反映花苗品质的高低),将每株所得的综合评分制成如图所示的频率分布直方图:
株,对每株进行综合评分(评分的高低反映花苗品质的高低),将每株所得的综合评分制成如图所示的频率分布直方图:
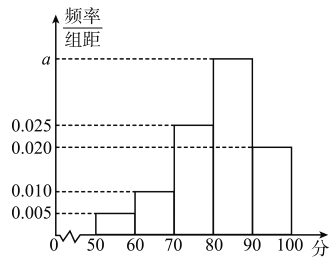
(1)求图中![]() 的值,并求综合评分的中位数;
的值,并求综合评分的中位数;
(2)记综合评分为![]() 及以上的花苗为优质花苗.填写下面的列联表,并判断是否有
及以上的花苗为优质花苗.填写下面的列联表,并判断是否有![]() 的把握认为优质花苗与培育方法有关.
的把握认为优质花苗与培育方法有关.
优质花苗 | 非优质花苗 | 合计 | |
甲培育法 |
| ||
乙培育法 |
| ||
合计 |
附:下面的临界值表仅供参考.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(参考公式: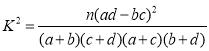 ,其中
,其中![]() .)
.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com