
科目: 来源: 题型:
【题目】对于函数![]() ,若存在实数m,使得
,若存在实数m,使得![]() 为R上的奇函数,则称
为R上的奇函数,则称![]() 是位差值为m的“位差奇函数”.
是位差值为m的“位差奇函数”.
(1)判断函数![]() 和
和![]() 是否是位差奇函数,并说明理由;
是否是位差奇函数,并说明理由;
(2)若![]() 是位差值为
是位差值为![]() 的位差奇函数,求
的位差奇函数,求![]() 的值;
的值;
(3)若对于任意![]() ,
,![]() 都不是位差值为m的位差奇函数,求实数t的取值范围.
都不是位差值为m的位差奇函数,求实数t的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() ,直线l不经过坐标原点O且不平行与坐标轴,l与
,直线l不经过坐标原点O且不平行与坐标轴,l与![]() 相交于A,B两点,线段
相交于A,B两点,线段![]() 的中点为M.
的中点为M.
(1)证明:直线![]() 的斜率与直线l的斜率的乘积为定值;
的斜率与直线l的斜率的乘积为定值;
(2)若直线l过点![]() ,延长线
,延长线![]() 与
与![]() 交于点P,若四边形
交于点P,若四边形![]() 是平行四边形,求直线l的斜率;
是平行四边形,求直线l的斜率;
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列![]() ,记集合
,记集合![]() .
.
(1)对于数列![]() ,写出集合
,写出集合![]() ;
;
(2)若![]() ,是否存在
,是否存在![]() ,使得
,使得![]() ?若存在,求出一组符合条件的
?若存在,求出一组符合条件的![]() ;若不存在,说明理由.
;若不存在,说明理由.
(3)若![]() ,把集合
,把集合![]() 中的元素从小到大排列,得到的新数列为
中的元素从小到大排列,得到的新数列为![]() ,若
,若![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() .
.
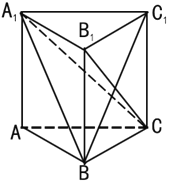
(1)求证:![]() 平面
平面![]() ;
;
(2)求异面直线![]() 与
与![]() 所成角的大小;
所成角的大小;
(3)点![]() 在线段
在线段![]() 上,且
上,且![]() ,点
,点![]() 在线段
在线段![]() 上,若
上,若![]() 平面
平面![]() ,求
,求![]() 的值(用含
的值(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年6月,国内的![]() 运营牌照开始发放.从
运营牌照开始发放.从![]() 到
到![]() ,我们国家的移动通信业务用了不到20年的时间,完成了技术上的飞跃,跻身世界先进水平.为了解高校学生对
,我们国家的移动通信业务用了不到20年的时间,完成了技术上的飞跃,跻身世界先进水平.为了解高校学生对![]() 的消费意愿,2019年8月,从某地在校大学生中随机抽取了1000人进行调查,样本中各类用户分布情况如下:
的消费意愿,2019年8月,从某地在校大学生中随机抽取了1000人进行调查,样本中各类用户分布情况如下:
用户分类 | 预计升级到 | 人数 |
早期体验用户 | 2019年8月至2019年12月 | 270人 |
中期跟随用户 | 2020年1月至2021年12月 | 530人 |
后期用户 | 2022年1月及以后 | 200人 |
我们将大学生升级![]() 时间的早晚与大学生愿意为
时间的早晚与大学生愿意为![]() 套餐支付更多的费用作比较,可得出下图的关系(例如早期体验用户中愿意为
套餐支付更多的费用作比较,可得出下图的关系(例如早期体验用户中愿意为![]() 套餐多支付5元的人数占所有早期体验用户的
套餐多支付5元的人数占所有早期体验用户的![]() ).
).

(1)从该地高校大学生中随机抽取1人,估计该学生愿意在2021年或2021年之前升级到![]() 的概率;
的概率;
(2)从样本的早期体验用户和中期跟随用户中各随机抽取1人,以![]() 表示这2人中愿意为升级
表示这2人中愿意为升级![]() 多支付10元或10元以上的人数,求
多支付10元或10元以上的人数,求![]() 的分布列和数学期望;
的分布列和数学期望;
![]() 套餐,能否认为样本中早期体验用户的人数有变化?说明理由.
套餐,能否认为样本中早期体验用户的人数有变化?说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】将初始温度为![]() 的物体放在室温恒定为
的物体放在室温恒定为![]() 的实验室里,现等时间间隔测量物体温度,将第
的实验室里,现等时间间隔测量物体温度,将第![]() 次测量得到的物体温度记为
次测量得到的物体温度记为![]() ,已知
,已知![]() .已知物体温度的变化与实验室和物体温度差成正比(比例系数为
.已知物体温度的变化与实验室和物体温度差成正比(比例系数为![]() ).给出以下几个模型,那么能够描述这些测量数据的一个合理模型为__________:(填写模型对应的序号)
).给出以下几个模型,那么能够描述这些测量数据的一个合理模型为__________:(填写模型对应的序号)
①![]() ;②
;②![]() ;③
;③![]() .
.
在上述模型下,设物体温度从![]() 升到
升到![]() 所需时间为
所需时间为![]() ,从
,从![]() 上升到
上升到![]() 所需时间为
所需时间为![]() ,从
,从![]() 上升到
上升到![]() 所需时间为
所需时间为![]() ,那么
,那么![]() 与
与![]() 的大小关系是________(用“
的大小关系是________(用“![]() ”,“
”,“![]() ”或“
”或“![]() ”号填空)
”号填空)
查看答案和解析>>
科目: 来源: 题型:
【题目】用平面截圆柱面,当圆柱的轴与![]() 所成角为锐角时,圆柱面的截面是一个椭圆,著名数学家
所成角为锐角时,圆柱面的截面是一个椭圆,著名数学家![]() 创立的双球实验证明了上述结论.如图所示,将两个大小相同的球嵌入圆柱内,使它们分别位于
创立的双球实验证明了上述结论.如图所示,将两个大小相同的球嵌入圆柱内,使它们分别位于![]() 的上方和下方,并且与圆柱面和
的上方和下方,并且与圆柱面和![]() 均相切.给出下列三个结论:
均相切.给出下列三个结论:
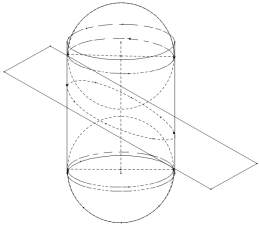
①两个球与![]() 的切点是所得椭圆的两个焦点;
的切点是所得椭圆的两个焦点;
②若球心距![]() ,球的半径为
,球的半径为![]() ,则所得椭圆的焦距为2;
,则所得椭圆的焦距为2;
③当圆柱的轴与![]() 所成的角由小变大时,所得椭圆的离心率也由小变大.
所成的角由小变大时,所得椭圆的离心率也由小变大.
其中,所有正确结论的序号是( )
A.①B.②③C.①②D.①②③
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为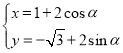 (其中
(其中![]() 为参数,
为参数,![]() ).在极坐标系(以坐标原点
).在极坐标系(以坐标原点![]() 为极点,以
为极点,以![]() 轴非负半轴为极轴)中,曲线
轴非负半轴为极轴)中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 上恰有一个点到曲线
上恰有一个点到曲线![]() 的距离为1,求曲线
的距离为1,求曲线![]() 的直角坐标方程.
的直角坐标方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com