
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为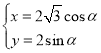 (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,且
,且![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,已知点
两点,已知点![]() 的极坐标为
的极坐标为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程,并求
的直角坐标方程,并求![]() 的值;
的值;
(2)若矩形![]() 内接于曲线
内接于曲线![]() 且四边与坐标轴平行,求其周长的最大值.
且四边与坐标轴平行,求其周长的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为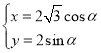 (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,且
,且![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,已知点
两点,已知点![]() 的极坐标为
的极坐标为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程,并求
的直角坐标方程,并求![]() 的值;
的值;
(2)若矩形![]() 内接于曲线
内接于曲线![]() 且四边与坐标轴平行,求其周长的最大值.
且四边与坐标轴平行,求其周长的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 四点都在抛物线
四点都在抛物线![]() 上.
上.
(1)若线段![]() 的斜率为
的斜率为![]() ,求线段
,求线段![]() 中点的纵坐标;
中点的纵坐标;
(2)记![]() ,若直线
,若直线![]() ,
,![]() 均过定点
均过定点![]() ,且
,且![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,证明:
的中点,证明:![]() ,
,![]() ,
,![]() 三点共线.
三点共线.
查看答案和解析>>
科目: 来源: 题型:
【题目】由于工作需要,某公司准备一次性购买两台具有智能打印、扫描、复印等多种功能的智能激光型打印机.针对购买后未来五年内的售后,厂家提供如下两种方案:
方案一:一次性缴纳![]() 元,在未来五年内,可免费上门维修
元,在未来五年内,可免费上门维修![]() 次,超过
次,超过![]() 次后每次收取费用
次后每次收取费用![]() 元;
元;
方案二:一次性缴纳![]() 元,在未来五年内,可免费上门维修
元,在未来五年内,可免费上门维修![]() 次,超过
次,超过![]() 次后每次收取费用
次后每次收取费用![]() 元.
元.
该公司搜集并整理了![]() 台这款打印机使用五年的维修次数,所得数据如下表所示:
台这款打印机使用五年的维修次数,所得数据如下表所示:
维修次数 |
|
|
|
|
台数 |
|
|
|
|
以这![]() 台打印机使用五年的维修次数的频率代替
台打印机使用五年的维修次数的频率代替![]() 台打印机使用五年的维修次数的概率,记
台打印机使用五年的维修次数的概率,记![]() 表示这两台智能打印机五年内共需维修的次数.
表示这两台智能打印机五年内共需维修的次数.
(1)求![]() 的分布列及数学期望;
的分布列及数学期望;
(2)以两种方案产生的维修费用的期望值为决策依据,写出你的选择,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】“公平正义”是社会主义和谐社会的重要特征,是社会主义法治理念的价值追求.“考试”作为一种公平公正选拔人才的有效途径,正被广泛采用.每次考试过后,考生最关心的问题是:自己的考试名次是多少?自已能否被录取?能获得什么样的职位? 某单位准备通过考试(按照高分优先录取的原则)录用![]() 名,其中
名,其中![]() 个高薪职位和
个高薪职位和![]() 个普薪职位.实际报名人数为
个普薪职位.实际报名人数为![]() 名,考试满分为
名,考试满分为![]() 分.(一般地,对于一次成功的考试来说,考试成绩应服从正态分布. )考试后考试成绩的部分统计结果如下:
分.(一般地,对于一次成功的考试来说,考试成绩应服从正态分布. )考试后考试成绩的部分统计结果如下:
考试平均成绩是![]() 分,
分,![]() 分及其以上的高分考生
分及其以上的高分考生![]() 名.
名.
(1)最低录取分数是多少?(结果保留为整数)
(2)考生甲的成绩为![]() 分,若甲被录取,能否获得高薪职位?若不能被录取,请说明理由.
分,若甲被录取,能否获得高薪职位?若不能被录取,请说明理由.
参考资料:(1)当![]() 时,令
时,令![]() ,则
,则![]() .
.
(2)当![]() 时,
时,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】正方体![]() 的棱长为
的棱长为![]() ,点
,点![]() 为棱
为棱![]() 的中点.下列结论:①线段
的中点.下列结论:①线段![]() 上存在点
上存在点![]() ,使得
,使得![]() 平面
平面![]() ;②线段
;②线段![]() 上存在点
上存在点![]() ,使
,使![]() 得平面
得平面![]() ;③平面
;③平面![]() 把正方体分成两部分,较小部分的体积为
把正方体分成两部分,较小部分的体积为![]() ,其中所有正确的序号是( )
,其中所有正确的序号是( )
A.①B.③C.①③D.①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com