【题目】如图，在三棱锥P-ABC中，已知，顶点P在平面ABC上的射影为的外接圆圆心.

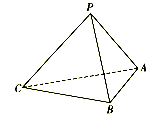
（1）证明：平面平面ABC；

（2）若点M在棱PA上，，且二面角P-BC-M的余弦值为，试求的值.

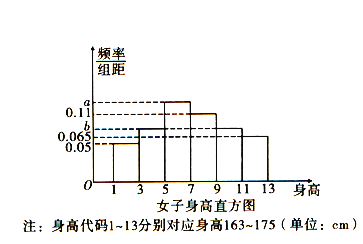
(1)求直方图中a，b的值；

(2)估计这个阵营女子身高的平均值 (同一组中的数据用该组区间的中点值为代表)

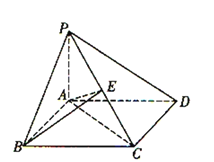
下列四个结论：①AB⊥AC；②AB⊥平面PAC；③PC⊥平面ABE；④BE⊥PC．正确的个数是( )

A.1B.2C.3D.4

A.n=360，m=14B.n=420，m=15C.n=540，m=18D.n=660，m=19

A.1150B.1380C.1610D.1860

【题目】某企业打算处理一批产品，这些产品每箱100件，以箱为单位销售.已知这批产品中每箱出现的废品率只有或者两种可能，两种可能对应的概率均为0.5.假设该产品正品每件市场价格为100元，废品不值钱.现处理价格为每箱8400元，遇到废品不予更换.以一箱产品中正品的价格期望值作为决策依据.

（1）在不开箱检验的情况下，判断是否可以购买；

（2）现允许开箱，有放回地随机从一箱中抽取2件产品进行检验.

①若此箱出现的废品率为，记抽到的废品数为，求的分布列和数学期望；

②若已发现在抽取检验的2件产品中，其中恰有一件是废品，判断是否可以购买.

【题目】如图，四边形与均为菱形，设与相交于点，若，且.

（1）求证：平面；

（2）求直线与平面所成角的余弦值.

【题目】以直角坐标系的原点为极点，x轴的非负半轴为极轴建立极坐标系，并在两种坐标系中取相同的长度单位已知直线l的参数方程为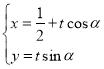(为参数，)，抛物线C的普通方程为.

(1)求抛物线C的准线的极坐标方程；

(2)设直线l与抛物线C相交于A，B两点，求的最小值及此时的值.

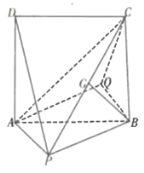
【题目】如图所示的几何体中，正方形所在平面垂直于平面，四边形为平行四边形，为上一点，且平面，.

（1）求证：平面平面；

（2）当三棱锥体积最大时，求直线与平面所成角的正切值.

【题目】【2018届安徽省合肥市高三第一次教学质量检测】一家大型购物商场委托某机构调查该商场的顾客使用移动支付的情况.调查人员从年龄在内的顾客中，随机抽取了180人，调查结果如表：

（1）为推广移动支付，商场准备对使用移动支付的顾客赠送1个环保购物袋.若某日该商场预计有12000人购物，试根据上述数据估计，该商场当天应准备多少个环保购物袋？

（2）某机构从被调查的使用移动支付的顾客中，按分层抽样的方式抽取7人作跟踪调查，并给其中2人赠送额外礼品，求获得额外礼品的2人年龄都在内的概率.