
科目: 来源: 题型:
【题目】数列![]() 满足
满足![]() .
.
①存在![]() 可以生成的数列
可以生成的数列![]() 是常数数列;
是常数数列;
②“数列![]() 中存在某一项
中存在某一项![]() ”是“数列
”是“数列![]() 为有穷数列”的充要条件;
为有穷数列”的充要条件;
③若![]() 为单调递增数列,则
为单调递增数列,则![]() 的取值范围是
的取值范围是![]() ;
;
④只要![]() ,其中
,其中![]() ,则
,则![]() 一定存在;
一定存在;
其中正确命题的序号为__________.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程
的参数方程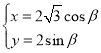 (
(![]() 为参数).直线
为参数).直线![]() 的参数方程
的参数方程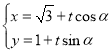 (
(![]() 为参数).
为参数).
(Ⅰ)求曲线![]() 在直角坐标系中的普通方程;
在直角坐标系中的普通方程;
(Ⅱ)以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,当曲线
轴的正半轴为极轴建立极坐标系,当曲线![]() 截直线
截直线![]() 所得线段的中点极坐标为
所得线段的中点极坐标为![]() 时,求直线
时,求直线![]() 的倾斜角.
的倾斜角.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两位同学参加诗词大赛,各答3道题,每人答对每道题的概率均为![]() ,且各人是否答对每道题互不影响.
,且各人是否答对每道题互不影响.
(Ⅰ)用![]() 表示甲同学答对题目的个数,求随机变量
表示甲同学答对题目的个数,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)设![]() 为事件“甲比乙答对题目数恰好多2”,求事件
为事件“甲比乙答对题目数恰好多2”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知曲线![]() ,
,![]() ,则下面结论正确的是( )
,则下面结论正确的是( )
A.把![]() 上各点的横坐标缩短到原来的
上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向右平移
倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
B.把![]() 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移
上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
C.把![]() 上各点的横坐标缩短到原来的
上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
D.把![]() 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移
上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
查看答案和解析>>
科目: 来源: 题型:
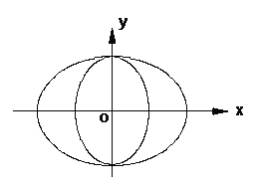
【题目】如图,曲线![]() 由两个椭圆
由两个椭圆![]() :
:![]() 和椭圆
和椭圆![]() :
:![]() 组成,当
组成,当![]() 成等比数列时,称曲线
成等比数列时,称曲线![]() 为“猫眼曲线”.
为“猫眼曲线”.
(1)若猫眼曲线![]() 过点
过点![]() ,且
,且![]() 的公比为
的公比为![]() ,求猫眼曲线
,求猫眼曲线![]() 的方程;
的方程;
(2)对于题(1)中的求猫眼曲线![]() ,任作斜率为
,任作斜率为![]() 且不过原点的直线与该曲线相交,交椭圆
且不过原点的直线与该曲线相交,交椭圆![]() 所得弦的中点为M,交椭圆
所得弦的中点为M,交椭圆![]() 所得弦的中点为N,求证:
所得弦的中点为N,求证:![]() 为与
为与![]() 无关的定值;
无关的定值;
(3)若斜率为![]() 的直线
的直线![]() 为椭圆
为椭圆![]() 的切线,且交椭圆
的切线,且交椭圆![]() 于点
于点![]() ,
,![]() 为椭圆
为椭圆![]() 上的任意一点(点
上的任意一点(点![]() 与点
与点![]() 不重合),求
不重合),求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在一条景观道的一端有一个半径为![]() 米的圆形摩天轮O,逆时针
米的圆形摩天轮O,逆时针![]() 分钟转一圈,从
分钟转一圈,从![]() 处进入摩天轮的座舱,
处进入摩天轮的座舱,![]() 垂直于地面
垂直于地面![]() ,在距离
,在距离![]() 处
处![]() 米处设置了一个望远镜
米处设置了一个望远镜![]() .
.

(1)同学甲打算独自乘坐摩天轮,但是其母亲不放心,于是约定在登上摩天轮座舱![]() 分钟后,在座舱内向其母亲挥手致意,而其母亲则在望远镜
分钟后,在座舱内向其母亲挥手致意,而其母亲则在望远镜![]() 中仔细观看.问望远镜
中仔细观看.问望远镜![]() 的仰角
的仰角![]() 应调整为多少度?(精确到1度)
应调整为多少度?(精确到1度)
(2)在同学甲向其母亲挥手致意的同时,同一座舱的另一名乘客乙在拍摄地面上的一条绿化带![]() ,发现取景的视角
,发现取景的视角![]() 恰为
恰为![]() ,求绿化带
,求绿化带![]() 的长度(精确到1米)
的长度(精确到1米)
查看答案和解析>>
科目: 来源: 题型:
【题目】某农场规划将果树种在正方形的场地内.为了保护果树不被风吹,决定在果树的周围种松树. 在下图里,你可以看到规划种植果树的列数(n),果树数量及松树数量的规律:

(1)按此规律,n = 5时果树数量及松树数量分别为多少;并写出果树数量![]() ,及松树数量
,及松树数量![]() 关于n的表达式
关于n的表达式
(2)定义:![]()
![]() 为
为![]() 增加的速度;现农场想扩大种植面积,问:哪种树增加的速度会更快?并说明理由
增加的速度;现农场想扩大种植面积,问:哪种树增加的速度会更快?并说明理由
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某人打算做一个正四棱锥形的金字塔模型,先用木料搭边框,再用其他材料填充,已知金字塔的每一条棱和边都相等.
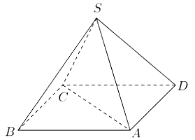
(1)求证:直线AC垂直于直线SD;
(2)若搭边框共使用木料24米,则需要多少立方米的填充材料才能将整个金字塔内部填满?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() (
(![]() 为常数,
为常数,![]() 且
且![]() ),且数列
),且数列![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列.
的等差数列.
(1)求证:数列![]() 是等比数列;
是等比数列;
(2)若![]() ,当
,当![]() 时,求数列
时,求数列![]() 的前
的前![]() 项和
项和![]() 的最小值;
的最小值;
(3)若![]() ,问是否存在实数
,问是否存在实数![]() ,使得
,使得![]() 是递增数列?若存在,求出
是递增数列?若存在,求出![]() 的范围;若不存在,说明理由.
的范围;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com