
科目: 来源: 题型:
【题目】已知等比数列![]() 的首项
的首项![]() ,数列
,数列![]() 前
前![]() 项和记为
项和记为![]() ,前
,前![]() 项积记为
项积记为![]() .
.
(1) 若![]() ,求等比数列
,求等比数列![]() 的公比
的公比![]() ;
;
(2) 在(1)的条件下,判断![]() 与
与![]() 的大小;并求
的大小;并求![]() 为何值时,
为何值时,![]() 取得最大值;
取得最大值;
(3) 在(1)的条件下,证明:若数列![]() 中的任意相邻三项按从小到大排列,则总可以使其成等差数列;若所有这些等差数列的公差按从小到大的顺序依次记为
中的任意相邻三项按从小到大排列,则总可以使其成等差数列;若所有这些等差数列的公差按从小到大的顺序依次记为![]() ,则数列
,则数列![]() 为等比数列.
为等比数列.
查看答案和解析>>
科目: 来源: 题型:
【题目】对于函数![]() ,若在定义域内存在实数
,若在定义域内存在实数![]() ,满足
,满足![]() ,则称
,则称![]() 为“局部奇函数”.
为“局部奇函数”.
(1)已知二次函数![]() ,试判断
,试判断![]() 是否为“局部奇函数”?并说明理由;
是否为“局部奇函数”?并说明理由;
(2)若![]() 是定义在区间
是定义在区间![]() 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数![]() 的取值范围;
的取值范围;
(3)若![]() 为定义域
为定义域![]() 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数![]() 的取值范围;
的取值范围;
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的右顶点、上顶点分别为A、B,坐标原点到直线AB的距离为
的右顶点、上顶点分别为A、B,坐标原点到直线AB的距离为![]() ,且
,且![]() .
.

(1)求椭圆C的方程;
(2)过椭圆C的左焦点![]() 的直线
的直线![]() 交椭圆于M、N两点,且该椭圆上存在点P,使得四边形MONP(图形上字母按此顺序排列)恰好为平行四边形,求直线
交椭圆于M、N两点,且该椭圆上存在点P,使得四边形MONP(图形上字母按此顺序排列)恰好为平行四边形,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点P(1,2)在抛物线C:y2=2px(p>0)上.
(Ⅰ)求C的方程;
(Ⅱ)斜率为﹣1的直线与C交于异于点P的两个不同的点M,N,若直线PM,PN分别与x轴交于A,B两点,求证:△PAB为等腰三角形.
查看答案和解析>>
科目: 来源: 题型:
【题目】某中学的甲、乙、丙三名同学参加高校自主招生考试,每位同学彼此独立的从![]() 四所高校中选2所.
四所高校中选2所.
(Ⅰ)求甲、乙、丙三名同学都选![]() 高校的概率;
高校的概率;
(Ⅱ)若已知甲同学特别喜欢![]() 高校,他必选
高校,他必选![]() 校,另在
校,另在![]() 三校中再随机选1所;而同学乙和丙对四所高校没有偏爱,因此他们每人在四所高校中随机选2所.
三校中再随机选1所;而同学乙和丙对四所高校没有偏爱,因此他们每人在四所高校中随机选2所.
(ⅰ)求甲同学选![]() 高校且乙、丙都未选
高校且乙、丙都未选![]() 高校的概率;
高校的概率;
(ⅱ)记![]() 为甲、乙、丙三名同学中选
为甲、乙、丙三名同学中选![]() 校的人数,求随机变量
校的人数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在六棱锥P﹣ABCDEF中,六边形ABCDEF为正六边形,平面PAB⊥平面ABCDEF,AB=1,PA![]() ,PB=2.
,PB=2.
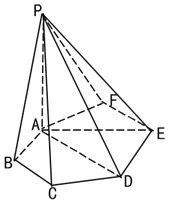
(1)求证:PA⊥平面ABCDEF;
(2)求直线PD与平面PAE所成角的正弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列{an}为等差数列,a1=1,前n项和为Sn,数列{bn}为等比数列,b1>1,公比为2,且b2S3=54,b3+S2=16.
(Ⅰ)求数列{an}与{bn}的通项公式;
(Ⅱ)设数列{cn}满足cn=an+bn,求数列{cn}的前n项和Tn.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知项数为![]() 的数列
的数列![]() 满足如下条件:①
满足如下条件:①![]() ;②
;②![]() .若数列
.若数列![]() 满足
满足![]() ,其中
,其中![]() ,则称
,则称![]() 为
为![]() 的“伴随数列”.
的“伴随数列”.
(1)数列1,3,5,7,9是否存在“伴随数列”,若存在,写出其“伴随数列”;若不存在,请说明理由;
(2)若![]() 为
为![]() 的“伴随数列”,证明:
的“伴随数列”,证明:![]() ;
;
(3)已知数列![]() 存在“伴随数列”
存在“伴随数列”![]() ,且
,且![]() ,
,![]() ,求m的最大值.
,求m的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com