
科目: 来源: 题型:
【题目】有次水下考古活动中,潜水员需潜入水深为30米的水底进行作业,其用氧量包含以下三个方面:①下潜时,平均速度为每分钟![]() 米,每分钟的用氧量为
米,每分钟的用氧量为![]() 升;②水底作业需要10分钟,每分钟的用氧量为0.3升;③返回水面时,速度为每分钟
升;②水底作业需要10分钟,每分钟的用氧量为0.3升;③返回水面时,速度为每分钟![]() 米,每分钟用氧量为0.2升;设潜水员在此次考古活动中的总用氧量为
米,每分钟用氧量为0.2升;设潜水员在此次考古活动中的总用氧量为![]() 升;
升;
(1)将![]() 表示为
表示为![]() 的函数;
的函数;
(2)若![]() ,求总用氧量
,求总用氧量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,
,![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(Ⅰ)若曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,求实数
垂直,求实数![]() 的值;
的值;
(Ⅱ)求函数![]() 的单调区间;
的单调区间;
(Ⅲ)用![]() 表示
表示![]() ,
,![]() 中的较大者,记函数
中的较大者,记函数![]() .若函数
.若函数![]() 在
在![]() 内恰有2个零点,求实数
内恰有2个零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() .
.
(Ⅰ)求椭圆![]() 的方程,并求其离心率;
的方程,并求其离心率;
(Ⅱ)过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,设点
,设点![]() 为第四象限内一点且在椭圆
为第四象限内一点且在椭圆![]() 上(点
上(点![]() 不在直线
不在直线![]() 上),直线
上),直线![]() 关于
关于![]() 的对称直线
的对称直线![]() 与椭圆交于另一点
与椭圆交于另一点![]() .设
.设![]() 为坐标原点,判断直线
为坐标原点,判断直线![]() 与直线
与直线![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四棱柱ABCD-A1B1C1D1的底面为菱形,AA1⊥底面ABCD,∠BAD=120°,AB=2,E,F分别为CD,AA1的中点.
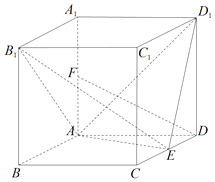
(Ⅰ)求证:DF∥平面B1AE;
(Ⅱ)若直线AD1与平面B1AE所成角的正弦值为![]() ,求AA1的长;
,求AA1的长;
(Ⅲ)在(Ⅱ)的条件下,求二面角B1-AE-D1的正弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校为了普及环保知识,增强学生的环保意识,在全校组织了一次有关环保知识的竞赛.经过初赛、复赛,甲、乙两个代表队(每队3人)进入了决赛,规定每人回答一个问题,答对为本队赢得10分,答错得0分.假设甲队中每人答对的概率均为![]() ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为![]() ,
,![]() ,
,![]() ,且各人回答正确与否相互之间没有影响,用
,且各人回答正确与否相互之间没有影响,用![]() 表示乙队的总得分.
表示乙队的总得分.
(Ⅰ)求![]() 的分布列及数学期望;
的分布列及数学期望;
(Ⅱ)求甲、乙两队总得分之和等于30分且甲队获胜的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() ,
,![]() ,…,
,…,![]() 是由
是由![]() (
(![]() )个整数
)个整数![]() ,
,![]() ,…,
,…,![]() 按任意次序排列而成的数列,数列
按任意次序排列而成的数列,数列![]() 满足
满足![]() (
(![]() ),
),![]() ,
,![]() ,…,
,…,![]() 是
是![]() ,
,![]() ,…,
,…,![]() 按从大到小的顺序排列而成的数列,记
按从大到小的顺序排列而成的数列,记![]() .
.
(1)证明:当![]() 为正偶数时,不存在满足
为正偶数时,不存在满足![]() (
(![]() )的数列
)的数列![]() .
.
(2)写出![]() (
(![]() ),并用含
),并用含![]() 的式子表示
的式子表示![]() .
.
(3)利用![]() ,证明:
,证明:![]() 及
及![]() .(参考:
.(参考:![]() .)
.)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() ),过原点的两条直线
),过原点的两条直线![]() 和
和![]() 分别与
分别与![]() 交于点
交于点![]() 、
、![]() 和
和![]() 、
、![]() ,得到平行四边形
,得到平行四边形![]() .
.
(1)当![]() 为正方形时,求该正方形的面积
为正方形时,求该正方形的面积![]() .
.
(2)若直线![]() 和
和![]() 关于
关于![]() 轴对称,
轴对称,![]() 上任意一点
上任意一点![]() 到
到![]() 和
和![]() 的距离分别为
的距离分别为![]() 和
和![]() ,当
,当![]() 为定值时,求此时直线
为定值时,求此时直线![]() 和
和![]() 的斜率及该定值.
的斜率及该定值.
(3)当![]() 为菱形,且圆
为菱形,且圆![]() 内切于菱形
内切于菱形![]() 时,求
时,求![]() ,
,![]() 满足的关系式.
满足的关系式.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() ,
,![]() ,
,![]() ,
,![]() 是各项均为正数的等差数列,其公差
是各项均为正数的等差数列,其公差![]() 大于零.若线段
大于零.若线段![]() ,
,![]() ,
,![]() ,
,![]() 的长分别为
的长分别为![]() ,
,![]() ,
,![]() ,
,![]() ,则( ).
,则( ).
A.对任意的![]() ,均存在以
,均存在以![]() ,
,![]() ,
,![]() 为三边的三角形
为三边的三角形
B.对任意的![]() ,均不存在以
,均不存在以![]() ,
,![]() ,
,![]() 为三边的三角形
为三边的三角形
C.对任意的![]() ,均存在以
,均存在以![]() ,
,![]() ,
,![]() 为三边的三角形
为三边的三角形
D.对任意的![]() ,均不存在以
,均不存在以![]() ,
,![]() ,
,为三边的三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com