
科目: 来源: 题型:
【题目】老王有一块矩形旧铁皮![]() ,其中
,其中![]() ,
,![]() ,他想充分利用这块铁皮制作一个容器,他有两个设想:设想1是沿矩形的对角线
,他想充分利用这块铁皮制作一个容器,他有两个设想:设想1是沿矩形的对角线![]() 把
把![]() 折起,使
折起,使![]() 移到
移到![]() 点,且
点,且![]() 在平面
在平面![]() 上的射影
上的射影![]() 恰好在
恰好在![]() 上,再利用新购铁皮缝制其余两个面得到一个三棱锥
上,再利用新购铁皮缝制其余两个面得到一个三棱锥![]() ;设想2是利用旧铁皮做侧面,新购铁皮做底面,缝制一个高为
;设想2是利用旧铁皮做侧面,新购铁皮做底面,缝制一个高为![]() ,侧面展开图恰为矩形
,侧面展开图恰为矩形![]() 的圆柱体;
的圆柱体;
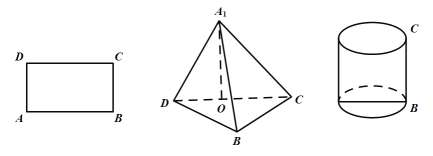
(1)求设想1得到的三棱锥![]() 中二面角
中二面角![]() 的大小;
的大小;
(2)不考虑其他因素,老王的设想1和设想2分别得到的几何体哪个容积更大?说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】设![]() 、
、![]() 、…、
、…、![]() 为平面
为平面![]() 内的
内的![]() 个点,在平面
个点,在平面![]() 内的所有点中,若点
内的所有点中,若点![]() 到
到![]() 、
、![]() 、…、
、…、![]() 点的距离之和最小,则称点
点的距离之和最小,则称点![]() 为
为![]() 、
、![]() 、…、
、…、![]() 点的一个“中位点”,有下列命题:①
点的一个“中位点”,有下列命题:①![]() 、
、![]() 、
、![]() 三个点共线,
三个点共线,![]() 在线段
在线段![]() 上,则
上,则![]() 是
是![]() 、
、![]() 、
、![]() 的中位点;②直角三角形斜边的中点是该直线三角形三个顶点的中位点;③若四个点
的中位点;②直角三角形斜边的中点是该直线三角形三个顶点的中位点;③若四个点![]() 、
、![]() 、
、![]() 、
、![]() 共线,则它们的中位点存在且唯一;④梯形对角线的交点是该梯形四个顶点的唯一中位点;其中的真命题是( )
共线,则它们的中位点存在且唯一;④梯形对角线的交点是该梯形四个顶点的唯一中位点;其中的真命题是( )
A.②④B.①②C.①④D.①③④
查看答案和解析>>
科目: 来源: 题型:
【题目】记实数![]() 、
、![]() 、
、![]() 、
、![]() 中的最大数为
中的最大数为![]() ,最小数为
,最小数为![]() .设
.设![]() 的三边边长分别为
的三边边长分别为![]() 、
、![]() 、
、![]() ,且
,且![]() ,定义
,定义![]() 的倾斜度为
的倾斜度为![]() .
.
(1)若![]() 为等腰三角形,则
为等腰三角形,则![]() _____;
_____;
(2)设![]() ,则
,则![]() 的取值范围是_____.
的取值范围是_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】设a,b,c为实数,f(x)=(x+a)(x2+bx+c),g(x)=(ax+1)(cx2+bx+1).记集合S={x|f(x)=0,x∈R},T={x|g(x)=0,x∈R}.若{S},{T}分别为集合S,T 的元素个数,则下列结论不可能的是( )
A.{S}=1且{T}=0B.{S}=1且{T}=1C.{S}=2且{T}=2D.{S}=2且{T}=3
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xoy中,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系。已知曲线C的极坐标方程为![]() ,过点
,过点![]() 的直线l的参数方程为
的直线l的参数方程为 (为参数),直线l与曲线C交于M、N两点。
(为参数),直线l与曲线C交于M、N两点。
(1)写出直线l的普通方程和曲线C的直角坐标方程:
(2)若![]() 成等比数列,求a的值。
成等比数列,求a的值。
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() .三角形
.三角形![]() 的两条边
的两条边![]() ,
,![]() 所在直线的斜率之积是
所在直线的斜率之积是![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)设直线![]() 方程为
方程为![]() ,直线
,直线![]() 方程为
方程为![]() ,直线
,直线![]() 交
交![]() 于
于![]() ,点
,点![]() ,
,![]() 关于
关于![]() 轴对称,直线
轴对称,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() .若
.若![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com