
科目: 来源: 题型:
【题目】国家每年都会对中小学生进行体质健康监测,一分钟跳绳是监测的项目之一.今年某小学对本校六年级300名学生的一分钟跳绳情况做了统计,发现一分钟跳绳个数最低为10,最高为189.现将跳绳个数分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 6组,并绘制出如下的频率分布直方图.
6组,并绘制出如下的频率分布直方图.
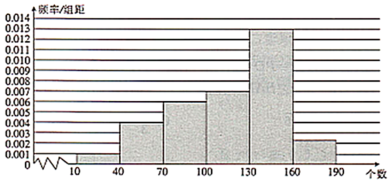
(1)若一分钟跳绳个数达到160为优秀,求该校六年级学生一分钟跳绳为优秀的人数;
(2)上级部门要对该校体质监测情况进行复查,发现每组男、女学生人数比例有很大差别,![]() 组男、女人数之比为
组男、女人数之比为![]() ,
,![]() 组男、女人数之比为
组男、女人数之比为![]() ,
,![]() 组男、女人数之比为
组男、女人数之比为![]() ,
,![]() 组男、女人数之比为
组男、女人数之比为![]() ,
,![]() 组男、女人数之比为
组男、女人数之比为![]() ,
,![]() 组男、女人数之比为
组男、女人数之比为![]() .试估计此校六年级男生一分钟跳绳个数的平均数(同一组中的数据用该组区间的中点值作代表,结果保留整数).
.试估计此校六年级男生一分钟跳绳个数的平均数(同一组中的数据用该组区间的中点值作代表,结果保留整数).
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年庆祝中华人民共和国成立70周年阅兵式彰显了中华民族从站起来、富起来迈向强起来的雄心壮志.阅兵式规模之大、类型之全均创历史之最,编组之新、要素之全彰显强军成就.装备方阵堪称“强军利刃”“强国之盾”,见证着人民军队迈向世界一流军队的坚定步伐.此次大阅兵不仅得到了全中国人的关注,还得到了无数外国人的关注.某单位有6位外国人,其中关注此次大阅兵的有5位,若从这6位外国人中任意选取2位做一次采访,则被采访者都关注了此次大阅兵的概率为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知直线![]() 与抛物线
与抛物线![]() :
:![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() 的面积为16(
的面积为16(![]() 为坐标原点).
为坐标原点).
(1)求![]() 的方程;
的方程;
(2)直线![]() 经过
经过![]() 的焦点
的焦点![]() 且
且![]() 不与
不与![]() 轴垂直,与
轴垂直,与![]() 交于
交于![]() ,
,![]() 两点,若线段
两点,若线段![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,证明:
,证明:![]() 为定值.
为定值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某工厂加工某种零件需要经过![]() ,
,![]() ,
,![]() 三道工序,且每道工序的加工都相互独立,三道工序加工合格的概率分别为
三道工序,且每道工序的加工都相互独立,三道工序加工合格的概率分别为![]() ,
,![]() ,
,![]() .三道工序都合格的零件为一级品;恰有两道工序合格的零件为二级品;其它均为废品,且加工一个零件为二级品的概率为
.三道工序都合格的零件为一级品;恰有两道工序合格的零件为二级品;其它均为废品,且加工一个零件为二级品的概率为![]() .
.
(1)求![]() ;
;
(2)若该零件的一级品每个可获利200元,二级品每个可获利100元,每个废品将使工厂损失50元,设一个零件经过三道工序加工后最终获利为![]() 元,求
元,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年庆祝中华人民共和国成立70周年阅兵式彰显了中华民族从站起来、富起来迈向强起来的雄心壮志.阅兵式规模之大、类型之全均创历史之最,编组之新、要素之全彰显强军成就.装备方阵堪称“强军利刃”“强国之盾”,见证着人民军队迈向世界一流军队的坚定步伐.此次大阅兵不仅得到了全中国人的关注,还得到了无数外国人的关注.某单位有10位外国人,其中关注此次大阅兵的有8位,若从这10位外国人中任意选取3位做一次采访,则被采访者中至少有2位关注此次大阅兵的概率为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,
,![]() .证明:
.证明:
(1)存在唯一x0∈(0,1),使f(x0)=0;
(2)存在唯一x1∈(1,2),使g(x1)=0,且对(1)中的x0,有x0+x1<2.
查看答案和解析>>
科目: 来源: 题型:
【题目】某工厂生产某种产品,为了控制质量,质量控制工程师要在产品出厂前对产品进行检验.现有![]() (
(![]() 且
且![]() )份产品,有以下两种检验方式:(1)逐份检验,则需要检验
)份产品,有以下两种检验方式:(1)逐份检验,则需要检验![]() 次;(2)混合检验,将这
次;(2)混合检验,将这![]() 份产品混合在一起作为一组来检验.若检测通过,则这
份产品混合在一起作为一组来检验.若检测通过,则这![]() 份产品全部为正品,因而这
份产品全部为正品,因而这![]() 份产品只要检验一次就够了;若检测不通过,为了明确这
份产品只要检验一次就够了;若检测不通过,为了明确这![]() 份产品究竟哪几份是次品,就要对这
份产品究竟哪几份是次品,就要对这![]() 份产品逐份检验,此时这
份产品逐份检验,此时这![]() 份产品的检验次数总共为
份产品的检验次数总共为![]() 次.假设在接受检验的样本中,每份样本的检验结果是正品还是次品都是独立的,且每份样本是次品的概率为
次.假设在接受检验的样本中,每份样本的检验结果是正品还是次品都是独立的,且每份样本是次品的概率为![]() .
.
(1)如果![]() ,采用逐份检验方式进行检验,求检测结果恰有两份次品的概率;
,采用逐份检验方式进行检验,求检测结果恰有两份次品的概率;
(2)现对![]() 份产品进行检验,运用统计概率相关知识回答:当
份产品进行检验,运用统计概率相关知识回答:当![]() 和
和![]() 满足什么关系时,用混合检验方式进行检验可以减少检验次数?
满足什么关系时,用混合检验方式进行检验可以减少检验次数?
(3)①当![]() (
(![]() 且
且![]() )时,将这
)时,将这![]() 份产品均分为两组,每组采用混合检验方式进行检验,求检验总次数
份产品均分为两组,每组采用混合检验方式进行检验,求检验总次数![]() 的数学期望;
的数学期望;
②当![]() (
(![]() ,且
,且![]() ,
,![]() )时,将这
)时,将这![]() 份产品均分为
份产品均分为![]() 组,每组采用混合检验方式进行检验,写出检验总次数
组,每组采用混合检验方式进行检验,写出检验总次数![]() 的数学期望(不需证明).
的数学期望(不需证明).
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右顶点分别为C、D,且过点
的左、右顶点分别为C、D,且过点![]() ,P是椭圆上异于C、D的任意一点,直线PC,PD的斜率之积为
,P是椭圆上异于C、D的任意一点,直线PC,PD的斜率之积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)O为坐标原点,设直线CP交定直线x = m于点M,当m为何值时,![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com