
科目: 来源: 题型:
【题目】如图,直四棱柱![]() 的底面
的底面![]() 是边长为2的菱形,
是边长为2的菱形,![]() ,
,![]() .
.![]() 、
、![]() 分别为
分别为![]() 和
和![]() 的中点.平面
的中点.平面![]() 与棱
与棱![]() 所在直线交于点
所在直线交于点![]() .
.
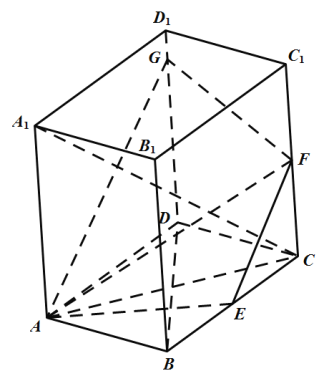
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)判断点![]() 是否与点
是否与点![]() 重合.
重合.
查看答案和解析>>
科目: 来源: 题型:
【题目】某电视台举行文艺比赛,并通过网络对比赛进行直播.比赛现场有5名专家评委给每位参赛选手评分,场外观众可以通过网络给每位参赛选手评分.每位选手的最终得分由专家评分和观众评分确定.某选手参与比赛后,现场专家评分情况如表;场外有数万名观众参与评分,将评分按照[7,8),[8,9),[9,10]分组,绘成频率分布直方图如图:
专家 | A | B | C | D | E |
评分 | 9.6 | 9.5 | 9.6 | 8.9 | 9.7 |
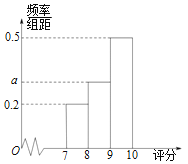
(1)求a的值,并用频率估计概率,估计某场外观众评分不小于9的概率;
(2)从5名专家中随机选取3人,X表示评分不小于9分的人数;从场外观众中随机选取3人,用频率估计概率,Y表示评分不小于9分的人数;试求E(X)与E(Y)的值;
(3)考虑以下两种方案来确定该选手的最终得分:方案一:用所有专家与观众的评分的平均数![]() 作为该选手的最终得分,方案二:分别计算专家评分的平均数
作为该选手的最终得分,方案二:分别计算专家评分的平均数![]() 和观众评分的平均数
和观众评分的平均数![]() ,用
,用![]() 作为该选手最终得分.请直接写出
作为该选手最终得分.请直接写出![]() 与
与![]() 的大小关系.
的大小关系.
查看答案和解析>>
科目: 来源: 题型:
【题目】2016年“一带一路”沿线64个国家GDP之和约为12.0万亿美元,占全球GDP的![]() ;人口总数约为32.1亿,占全球总人口的
;人口总数约为32.1亿,占全球总人口的![]() ;对外贸易总额(进口额+出口额)约为71885.6亿美元,占全球贸易总额的
;对外贸易总额(进口额+出口额)约为71885.6亿美元,占全球贸易总额的![]() .
.
2016年“一带一路”沿线国家情况
人口(万人) | GDP(亿美元) | 进口额(亿美元) | 出口额(亿美元) | |
蒙古 | 301.4 | 116.5 | 38.7 | 45.0 |
东南亚11国 | 63852.5 | 25802.2 | 11267.2 | 11798.6 |
南亚8国 | 174499.0 | 29146.6 | 4724.1 | 3308.5 |
中亚5国 | 6946.7 | 2254.7 | 422.7 | 590.7 |
西亚、北非19国 | 43504.6 | 36467.5 | 9675.5 | 8850.7 |
东欧20国 | 32161.9 | 26352.1 | 9775.5 | 11388.4 |
关于“一带一路”沿线国家2016年状况,能够从上述资料中推出的是( )
A.超过六成人口集中在南亚地区
B.东南亚和南亚国家GDP之和占全球的![]() 以上
以上
C.平均每个南亚国家对外贸易额超过1000亿美元
D.平均每个东欧国家的进口额高于平均每个西亚、北非国家的进口额
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() ,直线l的参数方程为
,直线l的参数方程为![]() (t为参数,
(t为参数,![]() ).
).
(1)写出直线l的普通方程和曲线C的直角坐标方程;
(2)若直线l与曲线C交于A,B两点,直线l的倾斜角![]() ,P点坐标为
,P点坐标为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的左,右焦点分别是
的左,右焦点分别是![]() ,
,![]() ,离心率为
,离心率为![]() ,直线
,直线![]() 被椭圆C截得的线段长为
被椭圆C截得的线段长为![]() .
.
(1)求椭圆C的方程;
(2)过点![]() 且斜率为k的直线l交椭圆C于A,B两点,交x轴于P点,点A关于x轴的对称点为M,直线BM交x轴于Q点.求证:
且斜率为k的直线l交椭圆C于A,B两点,交x轴于P点,点A关于x轴的对称点为M,直线BM交x轴于Q点.求证:![]() (O为坐标原点)为常数.
(O为坐标原点)为常数.
查看答案和解析>>
科目: 来源: 题型:
【题目】中国大学先修课程,是在高中开设的具有大学水平的课程,旨在让学有余力的高中生早接受大学思维方式、学习方法的训练,为大学学习乃至未来的职业生涯做好准备.某高中开设大学先修课程已有两年,两年共招收学生2000人,其中有300人参与学习先修课程,两年全校共有优等生200人,学习先修课程的优等生有60人.这两年学习先修课程的学生都参加了考试,并且都参加了某高校的自主招生考试(满分100分),结果如下表所示:
分数 |
|
|
|
|
|
人数 | 20 | 55 | 105 | 70 | 50 |
参加自主招生获得通过的概率 | 0.9 | 0.8 | 0.6 | 0.5 | 0.4 |
(1)填写列联表,并画出列联表的等高条形图,并通过图形判断学习先修课程与优等生是否有关系,根据列联表的独立性检验,能否在犯错误的概率不超过0.01的前提下认为学习先修课程与优等生有关系?
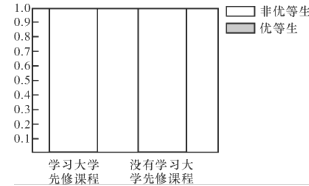
优等生 | 非优等生 | 总计 | |
学习大学先修课程 | |||
没有学习大学先修课程 | |||
总计 |
(2)已知今年有150名学生报名学习大学先修课程,以前两年参加大学先修课程学习成绩的频率作为今年参加大学先修课程学习成绩的概率.
①在今年参与大学先修课程的学生中任取一人,求他获得某高校自主招生通过的概率;
②设今年全校参加大学先修课程的学生获得某高校自主招生通过的人数为![]() ,求
,求![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
参考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在三棱锥![]() 中,
中,![]() 为等腰直角三角形,
为等腰直角三角形,![]() 为等边三角形,其中O为BC中点,且
为等边三角形,其中O为BC中点,且![]() .
.
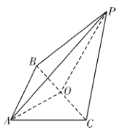
(1)求证:平面![]() 平面PBC;
平面PBC;
(2)若![]() 且
且![]() 平面EBC,其中E为AP上的点,求CE与平面ABC所成角的正弦值.
平面EBC,其中E为AP上的点,求CE与平面ABC所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com