
科目: 来源: 题型:
【题目】已知圆柱![]() 底面半径为1,高为
底面半径为1,高为![]() ,
,![]() 是圆柱的一个轴截面,动点
是圆柱的一个轴截面,动点![]() 从点
从点![]() 出发沿着圆柱的侧面到达点
出发沿着圆柱的侧面到达点![]() ,其距离最短时在侧面留下的曲线
,其距离最短时在侧面留下的曲线![]() 如图所示.将轴截面
如图所示.将轴截面![]() 绕着轴
绕着轴![]() 逆时针旋转
逆时针旋转![]() 后,边
后,边![]() 与曲线
与曲线![]() 相交于点
相交于点![]() .
.
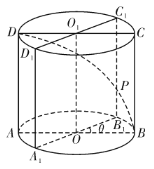
(1)求曲线![]() 的长度;
的长度;
(2)当![]() 时,求点
时,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】在水平地面上的不同两点处栽有两根笔直的电线杆,假设它们都垂直于地面,则在水平地面上视它们上端仰角相等的点![]() 的轨迹可能是( )
的轨迹可能是( )
①直线 ②圆 ③椭圆 ④抛物线
A.①②B.①③C.①②③D.②④
查看答案和解析>>
科目: 来源: 题型:
【题目】中国古代数学著作《算法统宗》中记载了这样的一个问题:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还”,其大意为:有一个人走了378里路,第一天健步行走,从第二天起其因脚痛每天走的路程为前一天的一半,走了6天后到达了目的地,问此人第三天走的路程里数为( )
A.192B.48C.24D.88
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() 有两个不同的极值点
有两个不同的极值点![]() .
.
(1)求![]() 的取值范围.
的取值范围.
(2)求![]() 的极大值与极小值之和的取值范围.
的极大值与极小值之和的取值范围.
(3)若![]() ,则
,则![]() 是否有最小值?若有,求出最小值;若没有,说明理由.
是否有最小值?若有,求出最小值;若没有,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点,
的左、右焦点,![]() 为该椭圆的一条垂直于
为该椭圆的一条垂直于![]() 轴的动弦,直线
轴的动弦,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与直线
与直线![]() 的交点为
的交点为![]() .
.
(1)证明:点![]() 恒在椭圆
恒在椭圆![]() 上.
上.
(2)设直线![]() 与椭圆
与椭圆![]() 只有一个公共点
只有一个公共点![]() ,直线
,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,在平面内是否存在定点
,在平面内是否存在定点![]() ,使得
,使得![]() 恒成立?若存在,求出该点坐标;若不存在,说明理由.
恒成立?若存在,求出该点坐标;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】生男生女都一样,女儿也是传后人.由于某些地区仍然存在封建传统思想,头胎的男女情况可能会影响生二孩的意愿,现随机抽取某地200户家庭进行调查统计.这200户家庭中,头胎为女孩的频率为0.5,生二孩的频率为0.525,其中头胎生女孩且生二孩的家庭数为60.
(1)完成下列![]() 列联表,并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关;
列联表,并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关;
生二孩 | 不生二孩 | 合计 | |
头胎为女孩 | 60 | ||
头胎为男孩 | |||
合计 | 200 |
(2)在抽取的200户家庭的样本中,按照分层抽样的方法在生二孩的家庭中抽取了7户,进一步了解情况,在抽取的7户中再随机抽取4户,求抽到的头胎是女孩的家庭户数![]() 的分布列及数学期望.
的分布列及数学期望.
附:
| 0.15 | 0.05 | 0.01 | 0.001 |
| 2.072 | 3.841 | 6.635 | 10.828 |
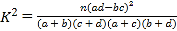 (其中
(其中![]() ).
).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,![]() 是正方形,点
是正方形,点![]() 在以
在以![]() 为直径的半圆弧上(
为直径的半圆弧上(![]() 不与
不与![]() ,
,![]() 重合),
重合),![]() 为线段
为线段![]() 的中点,现将正方形
的中点,现将正方形![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() .
.

(1)证明:![]() 平面
平面![]() .
.
(2)三棱锥![]() 的体积最大时,求二面角
的体积最大时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】南宋数学家杨辉在《详解九章算法》和《算法通变本末》中,提出了一些新的垛积公式,所讨论的高阶等差数列与一般等差数列不同,前后两项之差并不相等,但是逐项差数之差或者高次差成等差数列对这类高阶等差数列的研究,在杨辉之后一般称为“垛积术”.现有高阶等差数列,其前7项分别为1,4,8,14,23,36,54,则该数列的第19项为( )(注:![]() )
)
A.1624B.1024C.1198D.1560
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点,
的左、右焦点,![]() 为该椭圆的一条垂直于
为该椭圆的一条垂直于![]() 轴的动弦,直线
轴的动弦,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与直线
与直线![]() 的交点为
的交点为![]() .
.
(1)证明:点![]() 恒在椭圆
恒在椭圆![]() 上.
上.
(2)设直线![]() 与椭圆
与椭圆![]() 只有一个公共点
只有一个公共点![]() ,直线
,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,在平面内是否存在定点
,在平面内是否存在定点![]() ,使得
,使得![]() 恒成立?若存在,求出该点坐标;若不存在,说明理由.
恒成立?若存在,求出该点坐标;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】生男生女都一样,女儿也是传后人.由于某些地区仍然存在封建传统思想,头胎的男女情况可能会影响生二孩的意愿,现随机抽取某地200户家庭进行调查统计.这200户家庭中,头胎为女孩的频率为0.5,生二孩的频率为0.525,其中头胎生女孩且生二孩的家庭数为60.
(1)完成下列![]() 列联表,并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关;
列联表,并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关;
生二孩 | 不生二孩 | 合计 | |
头胎为女孩 | 60 | ||
头胎为男孩 | |||
合计 | 200 |
(2)在抽取的200户家庭的样本中,按照分层抽样的方法在头胎生女孩家庭中抽取了5户,进一步了解情况,在抽取的5户中再随机抽取3户,求这3户中恰好有2户生二孩的概率.
附:
| 0.15 | 0.05 | 0.01 | 0.001 |
| 2.072 | 3.841 | 6.635 | 10.828 |
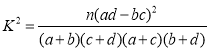 (其中
(其中![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com