
科目: 来源: 题型:
【题目】设椭圆![]() 的右顶点为
的右顶点为![]() ,上顶点为
,上顶点为![]() .已知椭圆的离心率为
.已知椭圆的离心率为![]() ,
,![]() .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设直线![]() :
:![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点,且点
两点,且点![]() 在第二象限.
在第二象限.![]() 与
与![]() 延长线交于点
延长线交于点![]() ,若
,若![]() 的面积是
的面积是![]() 面积的3倍,求
面积的3倍,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】红铃虫是棉花的主要害虫之一,能对农作物造成严重伤害,每只红铃虫的平均产卵数y和平均温度x有关,现收集了以往某地的7组数据,得到下面的散点图及一些统计量的值.(表中![]() )
)
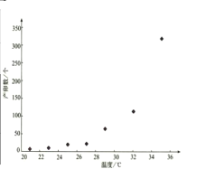
平均温度 | 21 | 23 | 25 | 27 | 29 | 32 | 35 | ||
平均产卵数 | 7 | 11 | 21 | 24 | 66 | 115 | 325 | ||
|
|
|
|
| |||||
27.429 | 81.286 | 3.612 | 40.182 | 147.714 | |||||
(1)根据散点图判断,![]() 与
与![]() (其中
(其中![]() 自然对数的底数)哪一个更适宜作为平均产卵数y关于平均温度x的回归方程类型?(给出判断即可,不必说明理由)并由判断结果及表中数据,求出y关x的回归方程.(计算结果精确到小数点后第三位)
自然对数的底数)哪一个更适宜作为平均产卵数y关于平均温度x的回归方程类型?(给出判断即可,不必说明理由)并由判断结果及表中数据,求出y关x的回归方程.(计算结果精确到小数点后第三位)
(2)根据以往统计,该地每年平均温度达到28℃以上时红铃虫会造成严重伤害,需要人工防治,其他情况均不需要人工防治,记该地每年平均温度达到28℃以上的概率为![]() .
.
①记该地今后5年中,恰好需要3次人工防治的概率为![]() ,求
,求![]() 的最大值,并求出相应的概率p.
的最大值,并求出相应的概率p.
②当![]() 取最大值时,记该地今后5年中,需要人工防治的次数为X,求X的数学期望和方差.
取最大值时,记该地今后5年中,需要人工防治的次数为X,求X的数学期望和方差.
附:线性回归方程系数公式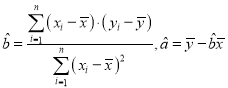 .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知动点![]() 到定点
到定点![]() 的距离之和为4.
的距离之和为4.
(1)求动点![]() 的轨迹方程
的轨迹方程![]()
(2)若轨迹![]() 与直线
与直线![]() 交于
交于![]() 两点,且
两点,且![]() 求
求![]() 的值.
的值.
(3)若点![]() 与点
与点![]() 在轨迹
在轨迹![]() 上,且点
上,且点![]() 在第一象限,点
在第一象限,点![]() 在第二象限,点
在第二象限,点![]() 与点
与点![]() 关于原点对称,求证:当
关于原点对称,求证:当![]() 时,三角形
时,三角形![]() 的面积为定值.
的面积为定值.
查看答案和解析>>
科目: 来源: 题型:
【题目】从抛物线![]() 上任意一点P向x轴作垂线段,垂足为Q,点M是线段
上任意一点P向x轴作垂线段,垂足为Q,点M是线段![]() 上的一点,且满足
上的一点,且满足![]()
(1)求点M的轨迹C的方程;
(2)设直线![]() 与轨迹c交于
与轨迹c交于![]() 两点,T为C上异于
两点,T为C上异于![]() 的任意一点,直线
的任意一点,直线![]() ,
,![]() 分别与直线
分别与直线![]() 交于
交于![]() 两点,以
两点,以![]() 为直径的圆是否过x轴上的定点?若过定点,求出符合条件的定点坐标;若不过定点,请说明理由.
为直径的圆是否过x轴上的定点?若过定点,求出符合条件的定点坐标;若不过定点,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某快递公司收取快递费用的标准是:重量不超过![]() 的包裹收费10元;重量超过
的包裹收费10元;重量超过![]() 的包裹,除收费10元之外,超过
的包裹,除收费10元之外,超过![]() 的部分,每超出
的部分,每超出![]() (不足
(不足![]() ,按
,按![]() 计算)需要再收费5元.该公司近60天每天揽件数量的频率分布直方图如下图所示(同一组数据用该区间的中点值作代表).
计算)需要再收费5元.该公司近60天每天揽件数量的频率分布直方图如下图所示(同一组数据用该区间的中点值作代表).
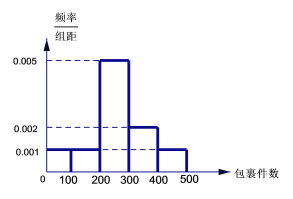
(1)求这60天每天包裹数量的平均值和中位数;
(2)该公司从收取的每件快递的费用中抽取5元作为前台工作人员的工资和公司利润,剩余的作为其他费用.已知公司前台有工作人员3人,每人每天工资100元,以样本估计总体,试估计该公司每天的利润有多少元?
(3)小明打算将![]() 四件礼物随机分成两个包裹寄出,且每个包裹重量都不超过
四件礼物随机分成两个包裹寄出,且每个包裹重量都不超过![]() ,求他支付的快递费为45元的概率.
,求他支付的快递费为45元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com