
科目: 来源: 题型:
【题目】市扶贫工作组从4男3女共7名成员中选出队长1人,副队长1人,普通队员2人组成4人工作小组下乡,要求工作组中至少有1名女同志,且队长和副队长不能都是女同志,共有______种安排方法.
查看答案和解析>>
科目: 来源: 题型:
【题目】西湖小学为了丰富学生的课余生活开设课后少年宫活动,其中面向二年级的学生共开设了三门课外活动课:七巧板、健美操、剪纸.203班有包括奔奔、果果在内的5位同学报名参加了少年宫活动,每位同学只能挑选一门课外活动课,已知每门课都有人选,则奔奔和果果选择了同一个课外活动课的选课方法种数为( )
A.18B.36C.72D.144
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两个商场同时出售一款西门子冰箱,其中甲商场位于老城区中心,乙商场位于高新区.为了调查购买者的年龄与购买冰箱的商场选择是否具有相关性,研究人员随机抽取了1000名购买此款冰箱的用户作调研,所得结果如表所示:
50岁以上 | 50岁以下 | |
选择甲商场 | 400 | 250 |
选择乙商场 | 100 | 250 |
(1)判断是否有![]() 的把握认为购买者的年龄与购买冰箱的商场选择具有相关性;
的把握认为购买者的年龄与购买冰箱的商场选择具有相关性;
(2)由于乙商场的销售情况未达到预期标准,商场决定给冰箱的购买者开展返利活动具体方案如下:当天卖出的前60台(含60台)冰箱,每台商家返利200元,卖出60台以上,超出60台的部分,每台返利50元.现将返利活动开展后15天内商场冰箱的销售情况统计如图所示:与此同时,老张得知甲商场也在开展返利活动,其日返利额的平均值为11000元,若老张将选择返利较高的商场购买冰箱,请问老张应当去哪个商场购买冰箱

附: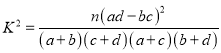 ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】将三棱锥![]() 与
与![]() 拼接得到如图所示的多面体,其中
拼接得到如图所示的多面体,其中![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() ,
,![]() 的中点,
的中点,![]() .
.
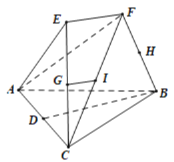
(1)当点![]() 在直线
在直线![]() 上时,证明:
上时,证明:![]() 平面
平面![]() ;
;
(2)若![]() 与
与![]() 均为面积为
均为面积为![]() 的等边三角形,求该多面体体积的最大值.
的等边三角形,求该多面体体积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】斐波那契数列0,1,1,2,3,5,8,13,…,是意大利数学家列昂纳多·斐波那契发明的,定义如下:![]() ,
,![]() ,
,![]() .某同学设计了一个求解斐波那契数列前
.某同学设计了一个求解斐波那契数列前![]() 项和的程序框图,如图所示,若输出
项和的程序框图,如图所示,若输出![]() 的值为232,则处理框和判断框中应该分别填入( )
的值为232,则处理框和判断框中应该分别填入( )

A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】谈祥柏先生是我国著名的数学科普作家,他写的《数学百草园》、《好玩的数学》、《故事中的数学》等书,题材广泛、妙趣横生,深受广大读者喜爱.下面我们一起来看《好玩的数学》中谈老的一篇文章《五分钟内挑出埃及分数》:文章首先告诉我们,古埃及人喜欢使用分子为1的分数(称为埃及分数).如用两个埃及分数![]() 与
与![]() 的和表示
的和表示![]() 等.从
等.从![]() 这100个埃及分数中挑出不同的3个,使得它们的和为1,这三个分数是________.(按照从大到小的顺序排列)
这100个埃及分数中挑出不同的3个,使得它们的和为1,这三个分数是________.(按照从大到小的顺序排列)
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数
为参数![]() ),以原点为极点,
),以原点为极点,![]() 轴非负半轴为极轴建立极坐标系,曲线
轴非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的焦点的极坐标;
的焦点的极坐标;
(2)若曲线![]() 的上焦点为
的上焦点为![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,
,![]() (
(![]() 为自然对数的底)。
为自然对数的底)。
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)若存在均属于区间![]() 的
的![]() ,
,![]() ,且
,且![]() ,使
,使![]() ,证明:
,证明:![]() ;
;
(Ⅲ)对于函数![]() 与
与![]() 定义域内的任意实数
定义域内的任意实数![]() ,若存在常数
,若存在常数![]() ,
,![]() ,使得
,使得![]() 和
和![]() 都成立,则称直线
都成立,则称直线![]() 为函数
为函数![]() 与
与![]() 的分界线。试探究当
的分界线。试探究当![]() 时,函数
时,函数![]() 与
与![]() 是否存在“分界线”?若存在,请给予证明,并求出
是否存在“分界线”?若存在,请给予证明,并求出![]() ,
,![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
查看答案和解析>>
科目: 来源: 题型:
【题目】设![]() 为常数,函数
为常数,函数![]() ,给出以下结论:
,给出以下结论:
(1)若![]() ,则
,则![]() 存在唯一零点
存在唯一零点
(2)若![]() ,则
,则![]()
(3)若![]() 有两个极值点
有两个极值点![]() ,则
,则![]()
其中正确结论的个数是( )
A. 3B. 2C. 1D. 0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com