
科目: 来源: 题型:
【题目】在极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,以极点为原点,以极轴所在直线为
,以极点为原点,以极轴所在直线为![]() 轴建立直角坐标系,曲线
轴建立直角坐标系,曲线![]() 分别与
分别与![]() 轴正半轴和
轴正半轴和![]() 轴正半轴交于点
轴正半轴交于点![]() ,
,![]() ,
,![]() 为直线
为直线![]() 上任意一点,点
上任意一点,点![]() 在射线
在射线![]() 上运动,且
上运动,且![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)求点![]() 轨迹围成的面积.
轨迹围成的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】现代足球运动是世上开展得最广泛、影响最大的运动项目,有人称它为“世界第一运动”.早在2000多年前的春秋战国时代,就有了一种球类游戏“蹴鞠”,后来经过阿拉伯人传到欧洲,发展成现代足球.1863年10月26日,英国人在伦敦成立了世界上第一个足球运动组织——英国足球协会,并统一了足球规则.人们称这一天是现代足球的诞生日.如图所示,足球表面是由若干黑色正五边形和白色正六边形皮围成的,我们把这些正五边形和正六边形都称为足球的面,任何相邻两个面的公共边叫做足球的棱.已知足球表面中的正六边形的面为20个,则该足球表面中的正五边形的面为______个,该足球表面的棱为______条.

查看答案和解析>>
科目: 来源: 题型:
【题目】关于圆周率![]() ,数学发展史上出现过许多很有创意的求法,如著名的蒲丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计
,数学发展史上出现过许多很有创意的求法,如著名的蒲丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计![]() 的值:先请
的值:先请![]() 名同学,每人随机写下一个都小于
名同学,每人随机写下一个都小于![]() 的正实数对
的正实数对![]() ,再统计两数能与
,再统计两数能与![]() 构成钝角三角形三边的数对
构成钝角三角形三边的数对![]() 的个数
的个数![]() ;最后再根据统计数m来估计
;最后再根据统计数m来估计![]() 的值.假如统计结果是
的值.假如统计结果是![]() 那么可以估计
那么可以估计![]() ______.
______.
查看答案和解析>>
科目: 来源: 题型:
【题目】“![]() 猜想”是指对于每一个正整数
猜想”是指对于每一个正整数![]() ,若
,若![]() 为偶数,则让它变成
为偶数,则让它变成![]() ;若
;若![]() 为奇数,则让它变成
为奇数,则让它变成![]() .如此循环,最终都会变成
.如此循环,最终都会变成![]() ,若数字
,若数字![]() 按照以上的规则进行变换,则变换次数为偶数的频率是( )
按照以上的规则进行变换,则变换次数为偶数的频率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】下表是某城市在2019年1月份至10月份各月最低温与最高温(℃)的数据表,已知该城市的各月最低温与最高温具有相关关系,根据该表,则下列结论错误的是( )
月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
最高温 | 5 | 9 | 9 | 11 | 17 | 24 | 27 | 30 | 31 | 21 |
最低温 |
|
| 1 |
| 7 | 17 | 19 | 23 | 25 | 10 |
A.最低温与最高温为正相关
B.每月最低温与最高温的平均值在前8个月逐月增加
C.月温差(最高温减最低温)的最大值出现在1月
D.1至4月温差(最高温减最低温)相对于7至10月,波动性更大
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,且
,且![]() ;数列
;数列![]() 的前n项和为
的前n项和为![]() ,且满足
,且满足![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)求数列![]() 的通项公式;
的通项公式;
(3)设![]() ,问:数列
,问:数列![]() 中是否存在不同两项
中是否存在不同两项![]() ,
,![]() (
(![]() ,i,
,i,![]() ),使
),使![]() 仍是数列
仍是数列![]() 中的项?若存在,请求出i,j;若不存在,请说明理由.
中的项?若存在,请求出i,j;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
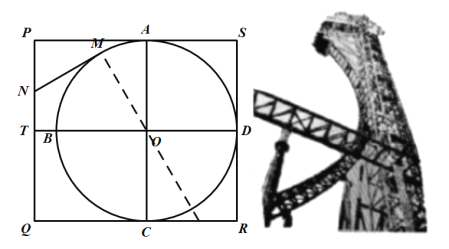
【题目】某游乐场过山车轨道在同一竖直钢架平面内,如图所示,矩形![]() 的长
的长![]() 为130米,宽
为130米,宽![]() 为120米,圆弧形轨道所在圆的圆心为0,圆O与
为120米,圆弧形轨道所在圆的圆心为0,圆O与![]() ,
,![]() ,
,![]() 分别相切于点A,D,CT为
分别相切于点A,D,CT为![]() 的中点.现欲设计过山车轨道,轨道由五段连接而成:出发点N在线段
的中点.现欲设计过山车轨道,轨道由五段连接而成:出发点N在线段![]() 上(不含端点,游客从点Q处乘升降电梯至点N),轨道第一段
上(不含端点,游客从点Q处乘升降电梯至点N),轨道第一段![]() 与圆O相切于点M,再沿着圆孤轨道
与圆O相切于点M,再沿着圆孤轨道![]() 到达最高点A,然后在点A处沿垂直轨道急速下降至点O处,接着沿直线轨道
到达最高点A,然后在点A处沿垂直轨道急速下降至点O处,接着沿直线轨道![]() 滑行至地面点G处(设计要求M,O,G三点共线),最后通过制动装置减速沿水平轨道
滑行至地面点G处(设计要求M,O,G三点共线),最后通过制动装置减速沿水平轨道![]() 滑行到达终点R记
滑行到达终点R记![]() 为
为![]() ,轨道总长度为l米.
,轨道总长度为l米.
(1)试将l表示为![]() 的函数
的函数![]() ,并写出
,并写出![]() 的取值范围;
的取值范围;
(2)求l最小时![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com